1. Desenvolva expressões para a densidade linear em termos do raio atômico R para as direções [100] e [111] na estrutura CFC.
2. Calcule e compare os valores da densidade linear para essas mesmas duas direções na prata.

Letra a:

Na figura abaixo é mostrada uma direção [100] dentro de uma célula unitária da CFC:

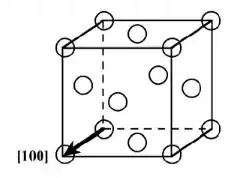
Para esta [100] direção, existe um átomo em cada um dos dois cantos da célula unitária e, portanto, existe o equivalente a 1 átomo centralizado no vetor de direção. O comprimento desse vetor de direção é apenas o comprimento da aresta da célula unitária, (Equação 3.1). Portanto, a expressão para a densidade linear deste plano é:

Uma célula unitária CFC dentro da qual é traçada uma direção [111] é mostrada abaixo:

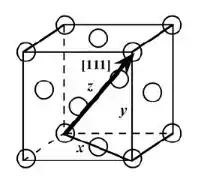
Para esta [111] direção, o vetor mostrado passa apenas pelos centros do átomo único em cada uma de suas extremidades e, portanto, existe a equivalência de 1 átomo centralizado no vetor de direção. O comprimento desse vetor de direção é indicado por z nesta figura, que é igual a:

onde x é o comprimento da face inferior diagonal, que é igual a 4R. Além disso, y é o comprimento da aresta da célula unitária, que é igual a (Equação 3.1). Assim, usando a equação acima, o comprimento z pode ser calculado da seguinte forma:

Portanto, a expressão para a densidade linear dessa direção é: