Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 18.Perguntas e Problemas - Ex. 19
Para os semicondutores intrínsecos, a concentração de portadores intrínsecos depende da temperatura da seguinte maneira:
ou, tomando os logaritmos naturais,
Dessa forma, um gráfico de ln em função de deve ser linear e ter uma inclinação de Considerando essa informação e os dados apresentados na Figura 18.16, determine a energia do espaçamento entre bandas para o silício e o germânio e compare esses valores com aqueles dados na Tabela 18.3.
Passo 1
Esse problema pede que façamos gráficos de ln ni versus temperatura recíproca para Si e Ge, usando os dados apresentados na Figura 18.16, e então determinamos a energia do gap band para cada material, percebendo que a inclinação da linha resultante é igual a . Abaixo é mostrado um gráfico para Si.
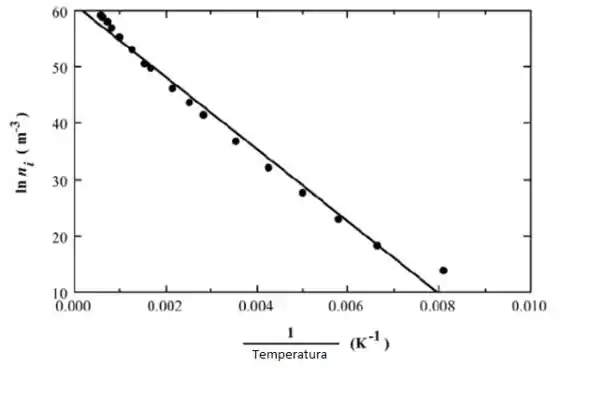
A inclinação da linha é igual a
Tomemos e ; seus valores correspondentes de ln são e ln . A incorporação desses valores na expressão acima leva a uma inclinação de
Esta inclinação leva a um valor de E:
Passo 2
O valor citado na Tabela 18.3 é 1.11 eV. Agora para Ge, um gráfico análogo é mostrado abaixo.
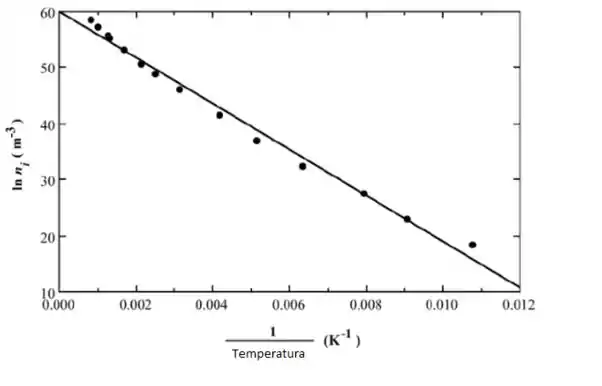
Calculamos os valores de energia do declive e da distância da banda da maneira descrita acima. Vamos tomar e ; seus valores correspondentes de ln η são ln e . Incorporar esses valores na expressão acima leva a uma inclinação de
Essa inclinação leva a um valor de
Este valor está de acordo com os 0,67 eV citados na Tabela 18.3.
Resposta
Este valor está de acordo com os 0,67 eV citados na Tabela 18.3.