No processo de fabricação de etanol, o mosto de fermentação é preparado a partir da diluição de melaço (mel final) com água ou com caldo de cana. As massas específicas e as concentrações em grau Brix desses fluidos são apresentadas na tabela a seguir. Grau Brix representa a porcentagem em massa de sólidos solúveis contida em soluções aquosas de açúcares ou fração mássica (). É uma medida indireta do teor de açúcares em soluções, uma vez que a maioria dos sólidos solúveis nesses fluidos são açúcares.

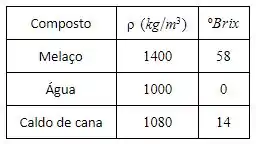
Supondo que a vazão de mosto que alimenta uma dorna de fermentação seja de e que o mesmo deva ter uma concentração de . Calcular as vazões de melaço e de água e de melaço e de caldo de cana, dependo do tipo da diluição (com água ou caldo) e as respectivas massas específicas dos mostos , supondo que a massa específica da mistura seja dada por:

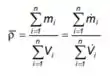
O fluxograma do processo de diluição com água ou caldo de cana (corrente 2) é ilustrado na Figura:

Lembrando que:

Substituindo os valores que temos nessa relação, podemos encontrar o :

Show! Agora podemos encontrar o e o , olha só:

Então o , será:

Agora vamos repetir o mesmo procedimento para a diluição do caldo de cana, beleza?

Para o caldo teremos:

Fazendo o balanço para os sólidos, temos:

Então:

Substituindo nossos dados:

Logo:

Agora substituindo o na equação, vamos ter:

Nossa relação de com agora fica:

E sendo assim o nosso , pode ser escrito como:

Usando a relação onde:

Podemos substituir o que descobrimos e teremos:

Sendo assim, vamos ter agora que e o , serão:

Agora o :

Uhul! Arrasamos!