Seja definida por
- Faça um esboço das curvas de nível de associadas aos níveis , e .
- Mostre que pertence a curva de nível
De associada ao nível .
Passo 1
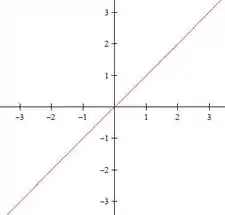
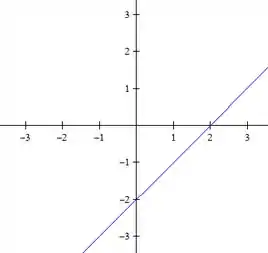
Bom, pra fazer as curvas de nível dessa função, precisamos apenas igualar a função ao nível pedido. Assim, para o nível , temos
Logo, temos a reta
Passo 2
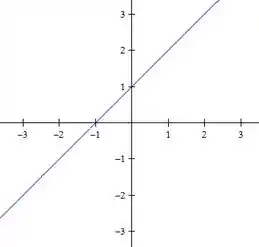
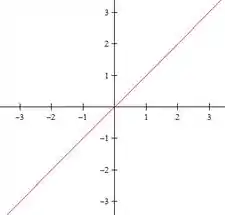
Agora vamos fazer para o nível
Temos então, duas retas:
Passo 3
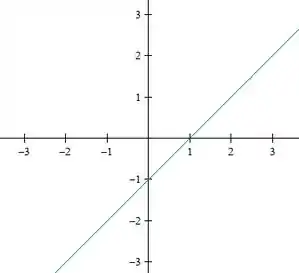
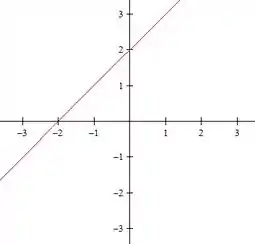
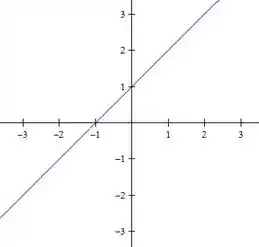
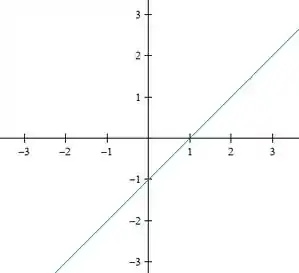
Para o ultimo nível, :
E, over and over again, temos duas retas:
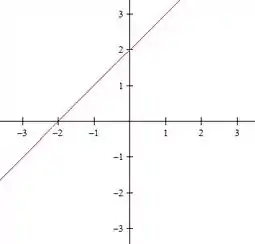
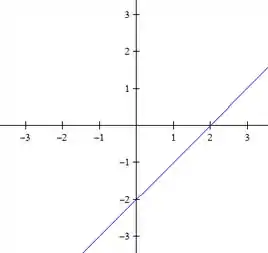
Passo 4
Para mostrar que o ponto pertence a curva de nível dessa função é só substituir esse ponto na função e vê se dá zero
Ou seja, o ponto pertence a curva de nível zero da função.
Repare que apenas olhando para a expressão que encontramos para o nível na letra
Já vemos que o ponto pertence a essa curva.
Resposta