Em uma escola com alunos, sabe-se que: jogam vôlei, jogam futebol e não praticam vôlei nem futebol. Nessas condições, determine quantos alunos praticam futebol e vôlei.
Passo 1
Vamos primeiro representar o que temos no diagrama de Venn:
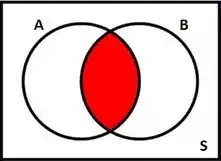
Em que é o conjunto dos alunos que jogam vôlei, é o conjunto dos alunos que jogam futebol e S é o conjunto de todos os alunos. Olha só o que fazemos agora:
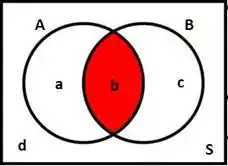
Então temos as seguintes relações:
Lembrando que .
Passo 2
Então agora podemos montar as equações:
Perceba que o que o problema quer é que você diga quantos alunos está na interseção dos conjuntos e , então queremos encontrar o valor de .
Passo 3
Vamos resolver então as equações:
Vamos começar somando as três primeiras equações:
E agora, vamos fazer essa equação menos a quarta equação do sistema:
Show, é isso aí!
Resposta
alunos praticam futebol e vôlei.