Crie uma classe chamada onde se o construtor receber três parâmetros deve-se calcular a solução de uma equação de segundo grau. Se receber dois parâmetros deve encontrar a solução para uma equação de primeiro grau quando a curva cruza o eixo .

Para fins de teste utilize e para a equação de primeiro grau, e utilize , e para a equação de segundo grau.

Vamos começar a nossa classe chamada . Pra começar vamos declarar os atributos da classe.

Todos os atributos estarão privados para garantir a integridade dos dados. Vamos precisar de três atributos e para receber os coeficientes das equações. Note que o atributo só será utilizado quando a equação tiver grau 2.

Também vamos declarar dois atributos e que conterão os resultados da equação. Da mesma forma, o atributo só será usado nas equações de segundo grau

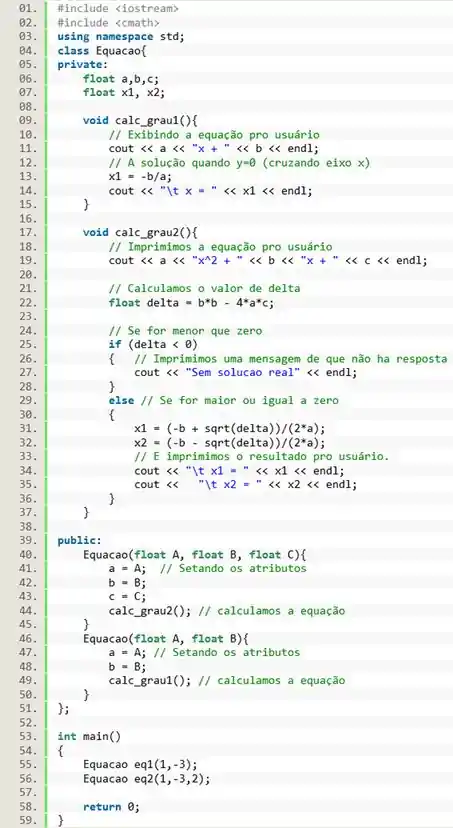
Vamos desenvolver um método do tipo que calcula o valor de quando a reta cruza o eixo das abscissas. Na linha 10 usamos um para exibir a equação para o usuário. Na linha 13 calculamos a raiz da equação e guardamos o resultado no atributo . Para concluir, na linha 14 usamos o para exibir o resultado pro usuário.

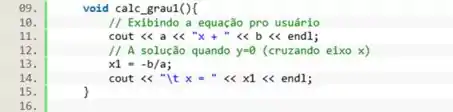
Vamos criar um segundo método do tipo que calcula a equação de segundo grau. Na linha 19 utilizamos a instrução para exibir a equação para o usuário.

Na linha 22 calculamos o valor de , note que declaramos uma nova variável dentro da função, pois ela só deve existir durante o cálculo.

Em seguida, usamos uma instrução para determinar quando é impossível obter soluções reais ou quando é possível obter soluções reais .

No primeiro caso, usamos o para informar o usuário. No segundo caso efetuamos os cálculos para encontrar as raízes, e exibimos os resultados.

Agora vamos pro coração da questão e desenvolver nossos métodos construtores.

Primeiro de tudo, precisamos mudar o contexto da classe de privado para público utilizando o

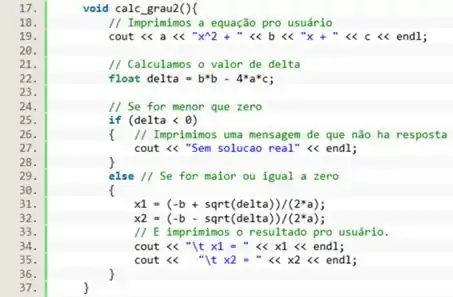
Precisamos definir um construtor para o caso de um objeto que recebe três valores no momento de sua criação. Começamos criando uma função sem tipo com o mesmo nome da classe, e que receba três parâmetros: e . Usaremos letras maiúsculas para não confundir com os atributos que definimos nos passos anteriores.

Em seguida, no corpo do construtor vamos utilizar os valores recebidos para setar os atributos da classe.

Com os valores dos atributos definidos, podemos chamar a função para efetuar o calcula e exibir os resultados pro usuário.

Seguindo os mesmos princípios, vamos criar uma sobrecarga para o construtor. Vamos criar uma segunda função sem tipo chamada mas que, desta vez, receba apenas dois parâmetros.

Da mesma forma, usaremos os valores recebidos para preencher os atributos da classe. Em seguida, vamos chamar o método para efetuar os cálculos.

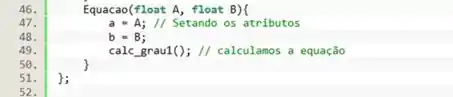
E isso conclui a nossa classe.

Antes de finalizar a questão, vamos executar os testes com os valores sugeridos pela questão:

Primeiro vamos criar um objeto chamado que calcule uma equação de primeiro grau com os valores e . E um segundo objeto chamado que calcule uma equação de segundo grau com os valores e

O resultado é: