Considere o diagrama de blocos da figura abaixo com as seguintes funções de transferência:
4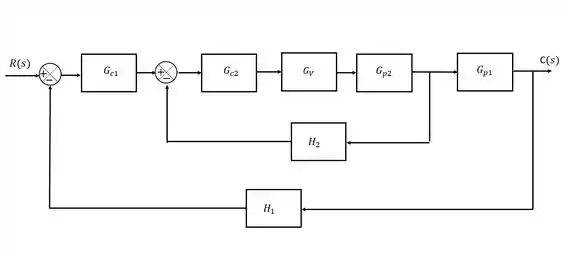
Determine o limite de estabilidade para um sistema de controle em cascada com dois controladores proporcionais. Assuma para o controlador secundário.
Passo 1
O exercício quer que a gente determine o limite de estabilidade do sistema, ou seja, ele quer que a gente diga queal o maior valor possível de para que o sistema continue estável. Ele já nos deu a dica de que ambos os controladores são do tipo proporcional, ou seja, a função se transferência dos controladores é do tipo:
Como já foi dado, precisamos apenas encontrar o valor máximo de .
Para conseguir encontrar esse limite, nós vamos precisar encontrar a função de transferência do sistema, porque com essa função dessa transferência conseguiremos tirar a equação característica da malha.
Então vamos tentar encontrar a função de transferência, mas vamos combinar que por enquanto não vamos trabalhar com números,porque isso vai facilitar a nossa vida.
Primeiramente então, vamos reduzir o loop interno em um só bloco:
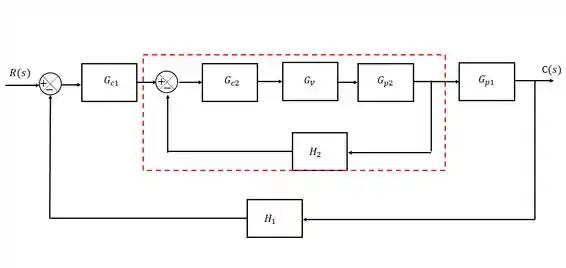
Aplicando a regra do loop:
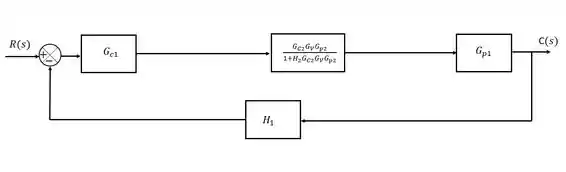
Ficamos então novamente com um loop simples, aí vamos aplicar novamente a regra do loop:
Essa regra do loop tá ensinada direitinho na aula de álgebra de diagrama de blocos. Se você tem dúvidas, ou não lembra como faz, seria bacana dar uma revisadinha nessa aula.
Rearranjando a expressão encontrada teremos a função de transferência da malha:
Passo 2
Agora que já temos a função de transferência, precisamos da equação característica. A equação característica nada mais é que o denominador da função de transferência da malha, ou seja:
Vamos agora finalmente substituir as expressões de funções de transferência dadas no enunciado do exercício:
Multiplicando os dois lados da expressão por :
Rearranjando:
Passo 3
Agora que já temos a equação carcterística, precisamos determinar o valor máxoma de Para isso, podemos usar o método da substituição direta ou o método de Routh-Hurwitz, o que você achar mais fácil.
Eu particularmente, prefiro o método da susbtituiçõa direta, então vou usar ele. Aplicando as substituições:
Podemos formar então um sistema com a parte real e a imaginária:
Resolvendo a parte imaginária:
Para encontrar o valor de basta substituir o valor de na expressão da parte real:
Logo o maior valor de ganho do controlador primário assumindo dois controladores proporcionais e que é 43,3