Deduza a função de transferência de uma malha de controle em cascata convencional:
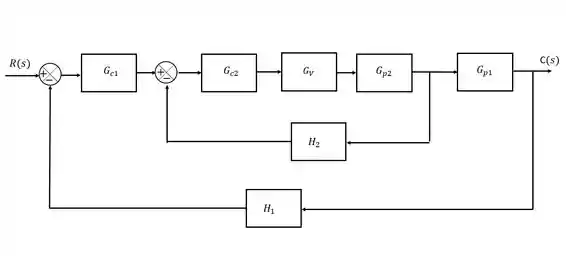
Passo 1
Se a gente reparar bem, a malha de controle em cascata pode ser interpretada como duas malhas feedback uma dentro da outra, então, para deduzir a função de transferência vamos nos aproveitar dessa característica.
Primeiramente, vamos olhar só para a malha de “dentro”, a malha secundária:
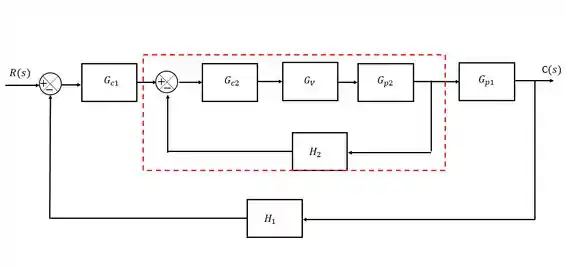
Todo o trecho destacado é uma malha feedback comum, e nós já vimos como se calcula a função de transferência dessa malha antes. Se você não lembra, é só lembrar da dica:
Essa e outras regras de álgebra do diagarama de blocos você pode revisar na nossa aula sobre o assunto aqui no Responde Aí!
Sendo assim, vamos reduzir todo o trecho destacado no diagarama acima em apenas um bloco, usando a regrinha aí de cima:
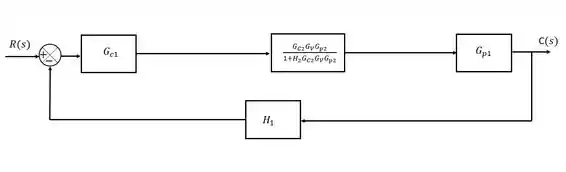
Passo 2
Agora que já reduzimos o primeiro loop, ficamos mais uma vez com um loop comum, e por isso, vamos usar a mesma regra que usamos ali em cima:
Portanto:
Multiplicando o numerador e o denominador po teremos: