Exercícios Resolvidos de Deformação em estruturas hiperestáticas – verificação do diagrama com carregamento externo
Ver TeoriaEnunciado
Para a viga abaixo, submetida ao carregamento mostrado, e com o seguinte diagrama de momentos fletores, determine o deslocamento vertical do ponto central.
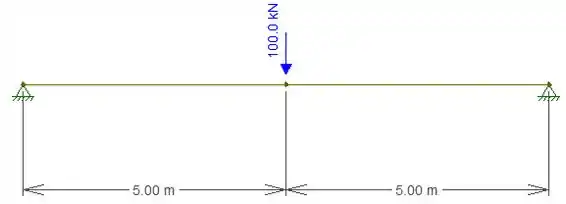
Passo 1
Se olharmos bem, podemos ver que o que de fato aconteceu foi que o diagrama de momentos fletores foi calculado na estrutura hiperestática, o que significa que estamos no caso 1 da nossa teoria, o que significa que devemos obrigatoriamente por a nossa carga unitária no sistema isostático, determinar o diagrama de momentos dessa carga, e usar a seguinte fórmula:
Já sabemos que como só temos momentos fletores, podemos ficar com apenas a integral de momentos fletores
e se tirarmos a parte constante da integral vamos ter que:
e sabemos que com essa integral basta que façamos apenas a combinação dos diagramas. Sendo assim vamos a segunda parte do problema.
Passo 2
Antes de tudo precisamos ter uma estrutura isostática, e para isso podemos quebrar o vínculo de momentos do apoio A. Sendo assim a nossa estrutura isostática será:
Aplicando um carregamento unitário vertical na nossa viga no ponto central obtemos que:
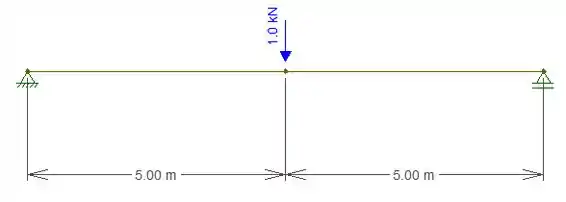
E agora precisamos combinar os dois diagramas para obtermos a deformação, mas devemos tomar alguns cuidados.
Passo 3
Sabemos que devemos fazer a seguinte combinação.
Aqui nós precisamos utilizar a tabela:
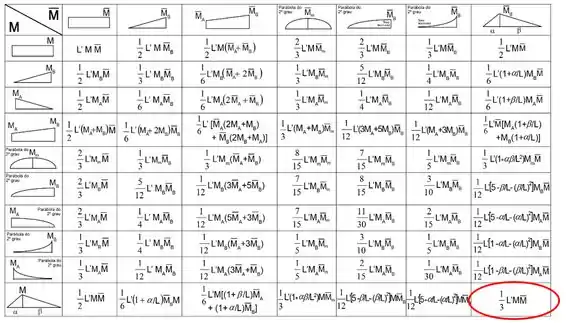
Dessa forma vamos obter:
Substituindo na equação vamos ter que: