O apoio em A da estrutura abaixo sofre um recalque vertical de 2cm e um recalque horizontal de 3cm. Sabendo disso determine o deslocamento horizontal do ponto B da estrutura. use
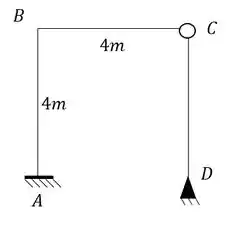
Passo 1
Aqui vamos usar um conceito novo. Para essa estrutura, sabemos facilmente que ela possuirá apenas 1 deslocabilidade interna no nó B, que iremos travar com uma chapa e teremos a seguinte estrutura:
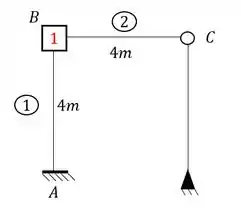
Porém perceba que o enunciado quer saber o quanto o ponto B irá se deslocar, ou seja, queremos saber o quanto o ponto B irá se movimentar, e sabemos que tudo que se movimenta no método dos deslocamentos deve ser travado. Ou seja, se queremos saber o quanto o ponto B irá se mover, devemos por nele um apoio do primeiro gênero, e com isso usa os conceitos de deslocabilidade da nossa estrutura para determinar o quanto ele de fato irá se mover.
Sendo assim teremos que:
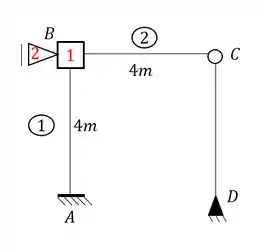
Perceba que a barra CD é bi-rotudada, ou seja, é como se fosse uma via bi-apoiada. O que significa isso? Significa que ela em nada vai contribuir nas nossas contas, ou seja, independente da deformação que ela tenha, ou da deformação imposta que façamos, a barra CD não vai contribuir nas contas, ou seja, uma simplificação que podemos fazer é:
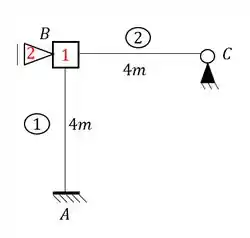
agora podemos continuar a conta ignorando essa barra, já que ela não vai contribuir em nada nas contas, e isso facilita os cálculos, a fórmula e o williot, então só temos a ganhar com isso, então bora lá.
Passo 2
Para podermos determinarmos a deformação precisamos antes de tudo determinar o williot da nossa estrutura. Para isso devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o ponot em C, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
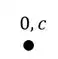
A partir desse ponto podemos marcar facilmente o ponto A, que desce 2 e anda 3 cm para esquerda, sendo assim o ponto A passa a ser.
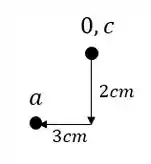
O ponto B vai ser achado a partir dos pontos A e C do nosso williot, usando o nosso conceito de ret perpendicular. Fazendo isso teremos que:
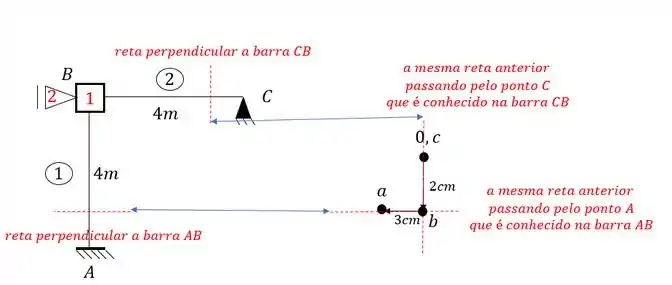
E assim determinamos o nosso wiliot completo que será dado por:
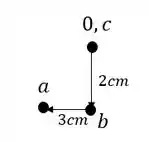
Passo 3
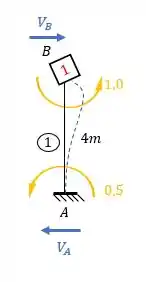
Tendo a deslocabilidade e o williot, podemos determinar o valor de . Como temos um apoio do primeiro gênero, temos que determinar as reações de apoio, e para isso precisamos determinar as deslocabilidades e momentos de cada barra, usando o nosso amigo williot teremos que:
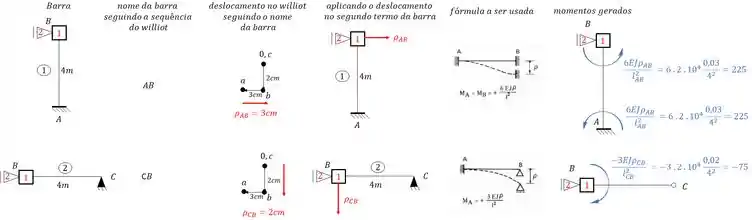
Os momentos que agem na chapa 1 iram gerar , sendo assim teremos que:
Perceba que somente uma barra (AB) será capaz de produzir reação de apoio na direaçaõ do apoio 2. E essa reação de apoio que precisamos para determinar . Sendo assim teremos que:
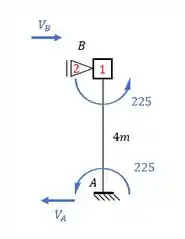
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 4
Vamos definir agora o valor de para termos o nosso sistema completo.
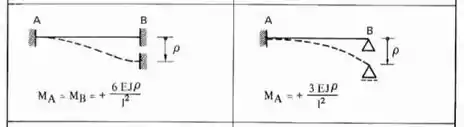
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso biengastado ou engastado e apoiado:
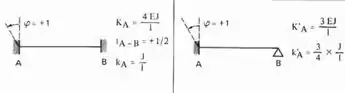
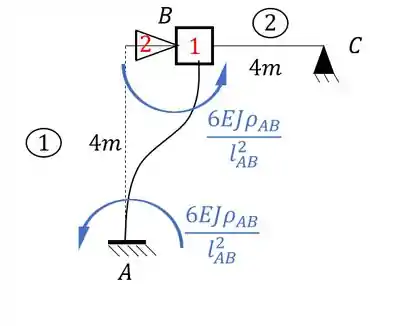
E rotacionando a chapa 1 e aplicando as equações teremos:
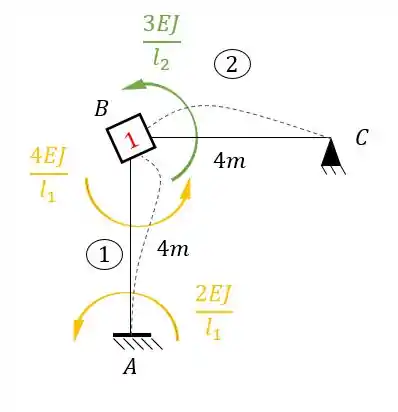
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Perceba que para determinar o valor de precisamos das reações de apoio que agem em 2. Podemos ver que de novo somente a barra AB produzira reações na direção horizontal, sendo assim teremos que:
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Sabemos aqui que temos que deslocar o apoio em 2, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso biengastado ou engastado e apoiado:
Causando o deslocamento teremos que:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E usando o valor de
E assim teremos:
Perceba que para determinar o valor de precisamos das reações de apoio que agem em 2. Podemos ver que de novo somente a barra AB produzira reações na direção horizontal, sendo assim teremos que:
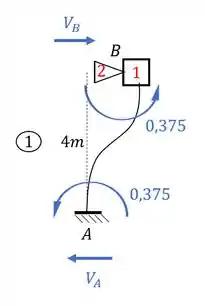
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 5
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que: