A proporção da população que pretende votar no candidato em uma dada eleição, é um parâmetro desconhecido e que só será revelado no dia da eleição. Assumindo que os eleitores não modifiquem suas intenções de voto, responda:

a) Deduzir detalhando todos os passos necessários para a construção do Intervalo de confiança – IC para a proporção.

b) Para um nível de confiança de 95%, qual é o erro máximo em pontos percentuais que podemos cometer com relação à estimativa da pesquisa, , calculada com uma amostra de tamanho ?

c) Qual deverá ser o tamanho da amostra para se ter um erro de no máximo ponto percentual, i.e. o comprimento do intervalo em cada lado do estimador da proporção ser inferior a , ao mesmo nível de confiança e para a mesma estimativa do item b)?

Para isso, consideramos uma amostra com variáveis aleatórias , , ..., , com . Cada uma dessas variáveis obedece a uma distribuição de Bernoulli: se a pessoa for a favor do candidato, a variável vale ; se ela não for, vale . Assim, definimos:

A soma vai representar o número de pessoas que é a favor do candidato nessa amostra, de modo que será a proporção de pessoas que apoiam o candidato nessa amostra. Note que faz o papel de . Para valores grandes de , a variável deve seguir uma distribuição aproximadamente normal (aqui estamos usando o teorema central do limite).

A ideia básica é que a soma de um número muito grande de variáveis aleatórias deve ter uma distribuição aproximadamente normal. Além disso,

Mas como cada variável segue uma distribuição de Bernoulli com parâmetro , temos que

Você deve lembrar que a média de uma distribuição de Bernoulli é , foi isso que eu usei na linha acima. Portanto,

Já para a variância, usamos que

Mas como , temos que

Uma outra forma de se deduzir isso é pensar que deve seguir uma binomial, de modo que

As duas formas de pensar estão corretas e são análogas!

Mas por que eu fiz tudo isso? Aqui vem o pulo do gato, presta bastante atenção...

Pelo teorema central do limite, a variável (que representa a proporção de eleitores a favor de um candidato) deve seguir uma distribuição normal e, no passo anterior, achamos sua média e sua variância:

Para uma distribuição normal, tudo que precisamos é sua média e sua variância: problema praticamente resolvido! Sabemos o valor de e usando o estimador de . Assim, pegando por exemplo ...

A partir daqui vou chamar e . O problema quer saber, com confiança seguro, qual o intervalo de valores de em torno da média que correspondem a essa probabilidade. Se ficou confuso eu vou desenhar para simplificar:

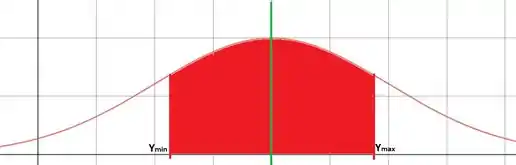
A linha verde representa a média . Queremos saber o intervalo que delimita a região pintada (entre e ) de modo que ela represente uma porcentagem tal da probabilidade total. Para isso, nós normalizamos a distribuição para que ela tenha média e desvio padrão , através da mudança de variável:

Com essa mudança de variável, a figura da distribuição passa a ser:

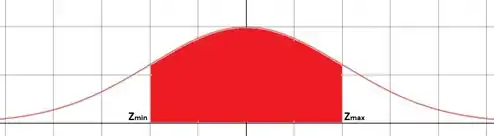
Como agora a distribuição é simétrica, é fácil ver que . Queremos que

Para determinar o valor de , temos que olhar para a tabela da distribuição normal padrão acumulada. Vou usar a versão que foi dada na própria prova:

Essa tabela pode ser fornecida de várias formas, por isso é bem importante saber qual a convenção que está sendo utilizada. Na tabela fornecida na prova, a distribuição acumulada representa a probabilidade de . Vamos adaptar nosso problema a essa situação:

Mas note que , pois representa metade da distribuição (que é simétrica). Assim,

Daí é só olhar na tabela, que podemos construir um bom intervalo de confiança!

b)

Para calcular o erro máximo, usamos a seguinte fórmula abaixo:

Sabemos que o nível de confiança é 95%, então:

Então, temos que...

Substituindo tudo na fórmula:

c)

Agora queremos descobrir para um de no máximo :

Logo, um tamanho legal da amostra é !