Arco-íris produzidos por gotas quadradas.
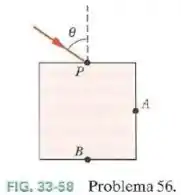
Suponha que, em um planeta exótico, as gotas de chuva tenham uma seção reta quadrada e caiam sempre com uma face paralela ao solo. A Fig.33-58 mostra uma dessas gostas, na qual incide um feixe de luz branca om um ângulo de incidência no ponto .
A parte da luz que penetra na gota se propaga até o ponto , onde parte é refratada de volta para o ar e a outra parte é refletida.
A luz refletida chega ao ponto , onde novamente parte da luz é refratada de volta para o ar e parte é refletida.
Qual é a diferença entre os ângulos dos raios de luz vermelha () e de luz azul () que deixam a gota:
- No ponto .
- No ponto B?
(Essa diferença faz com que um observador externo veja um arco-íris ao observar a luz que sai do ponto ou do ponto .)
Passo 1
Letra a)
Primeiro precisamos encontrar o ângulo de incidência da luz no ponto . Cada cor tem um ângulo de refração no ponto e logo seus ângulos de incidência são diferentes.
Os ângulos de refração do azul e do vermelho serão:
Os valores serão:
Passo 2
Com o ângulo de refração de cada cor, queremos agora os ângulos de incidência no ponto .
Esse ângulo vai ser .
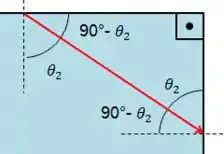
O ângulo de refração da luz que deixa a gota no ponto vai ser dado pela Lei de Snell novamente. Nesse caso:
Como e :
Vamos fazer para cada cor:
A dispersão angular na saída do ponto vai ser:
Passo 3
Letra b)
O ângulo de reflexão no ponto é igual ao ângulo de incidência, .
Porém, ao incidir no ponto , o ângulo de incidência será .
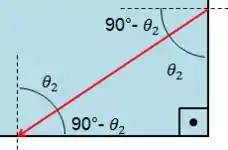
E nesse caso a lei de Snell ficará:
Mas calma lá. Vimos antes que:
Juntando as duas equações:
O que vale para todas as cores. Isso significa que as cores saem paralelas umas às outras no ponto e a dispersão é zero.
Resposta
Letra a)
Letra b)