Um feixe de luz de dois comprimentos de onda diferentes entra em uma lâmina de vidro de de espessura com um ângulo de incidência de Os índices de refração para as duas cores diferentes são e Devido à dispersão, os feixes coloridos, embora paralelos, são separados por uma pequena distância. Quanto vale essa distância?
Passo 1
Essa é uma questão de dispersão cromática: o índice de refração varia com o comprimento de onda e, por isso, as cores se separam! Vamos fazer um desenho da situação:
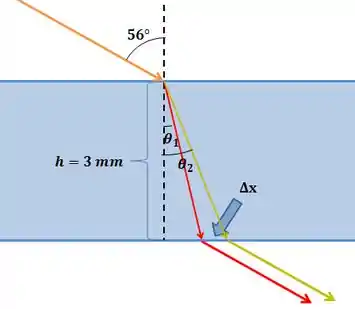
Queremos achar a distância entre as duas setas que estão saindo paralelas entre si! Essa distância vai ser , representado na figura abaixo:
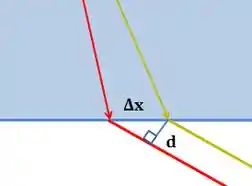
Vamos dar um passo de cada vez, com calma, para encontrar esta distância.
Passo 2
O primeiro passo é encontrar . Para isso, vamos achar a distância da linha tracejada até a primeira seta. Para isso, usando a tangente do ângulo, temos:
Precisamos então achar . Pela lei de Snell-Descartes:
Como então:
Pela nossa figura, é menor que . Isso implica em dizer que é maior que , pois quanto maior o índice de refração, menor o ângulo realizado com a normal. Por isso, iremos dizer que:
e
Substituindo:
Agora vamos fazer o mesmo raciocínio para a segunda seta, mais à direita.
Pela lei de Snell-Descartes:
Substituindo:
A distância entre os dois raios fica:
Passo 3
Por fim, temos que passar de para . Para isso, vamos lembrar que, quando os raios luminosos saem do vidro, eles saem paralelos ao raio que entra no vidro. Isso significa que o ângulo entre eles e a normal à superfície é .
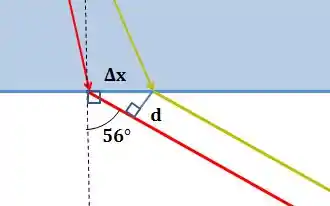
O que significa que os seus ângulos são:
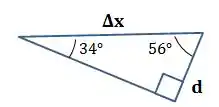
Por esse triângulo, podemos relacionar e pelo cosseno de .
A alternativa correta é a .
Resposta
Alternativa