Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 34
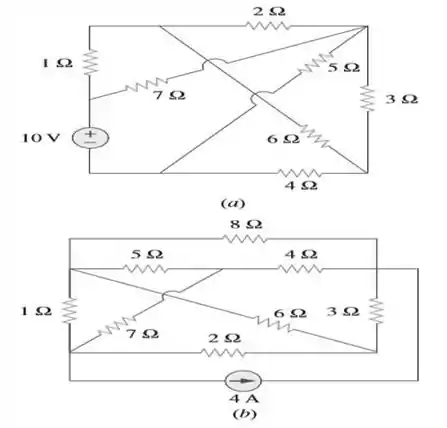
34. Determine qual dos circuitos da Figura é planar e redesenhe-o de modo a que não apresente ramos cruzados.
Passo 1
Designam-se por planares os circuitos cujo esquema elétrico é passível de representação num plano, sem que os seus ramos se intersectem mutuamente.
E com isso vamos dar início a nossa linha de pensamento.
Passo 2
a) Vamos ver se o primeiro circuito é planar. Bora nomear com pontinhos cada um dos nós desse circuito.
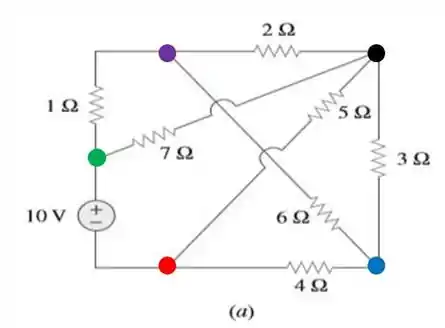
Podemos tirar algumas coisas interessantes desse circuito. As resistências de , e estão em série. A resistência de está em paralelo com as resistências de e , que estão em série. A resistência de está em paralelo com as resistências de e , que estão em série também.
E temos também que as resistências de , , e apontam para um mesmo nó.Com isso, temos informações suficientes para construir nosso circuito. E ele pode ser modificado para a seguinte forma:
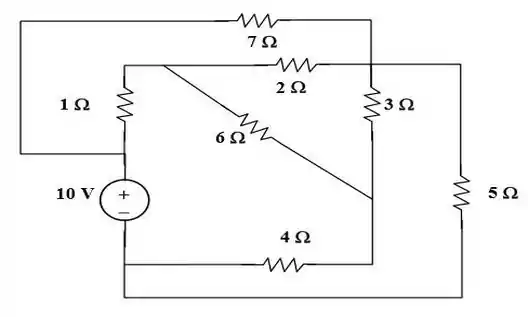
Que beleza! O nosso circuito é planar.
Passo 3
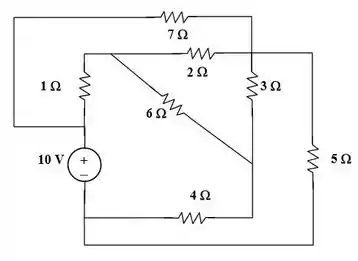
b) E no segundo circuito, bora fazer a mesma coisa que fizemos com o primeiro: nomear com pontinhos cada um dos nós desse circuito.
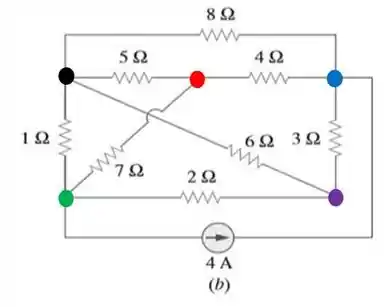
Olha só! Aquela resistência de no meio do circuito está fazendo conexão com três partes diferentes do circuito. De modo que é impossível obter um circuito sem o qual esse ramo se intercepte com outro ramo desse circuito. Logo, ele não é planar.
Resposta
a)
b)