Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 53
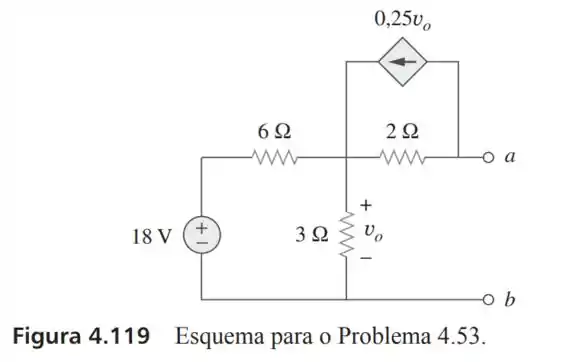
53- Determine o equivalente de Norton nos terminais do circuito da Figura
Passo 1
Vamos fechar as conexões e para encontrarmos a corrente de Norton.
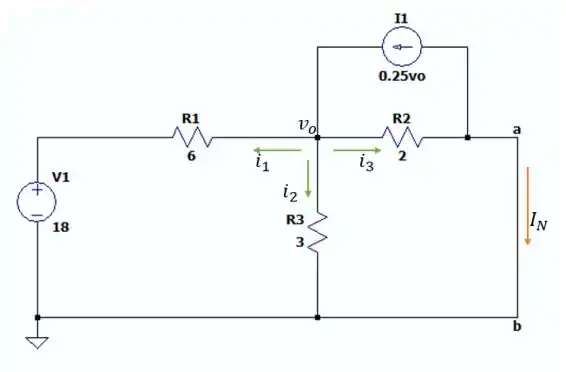
Aterrando o ponto nós temos a seguinte somatória de correntes no ponto onde temos a tensão de .
Tanto faz o sentido da corrente que você desenha, desde que você respeite na conta pois ele sai do ponto positivo e para em outro com sinal negativo.
Agora fazendo a somatória das correntes que chegam e saem do nó nós temos:
Passo 2
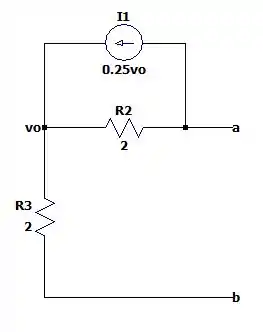
Agora vamos voltar com o circuito aberto para calcular a resistência de Thévenin.
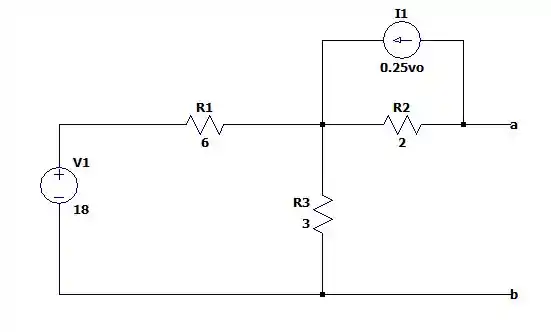
Por estar conectado no vazio a fonte de acaba não atuando no circuito, porém como existe uma tensão , a fonte dependente acabará existindo, mesmo ele estando conectando em . Nos deixando com um circuito igual a:
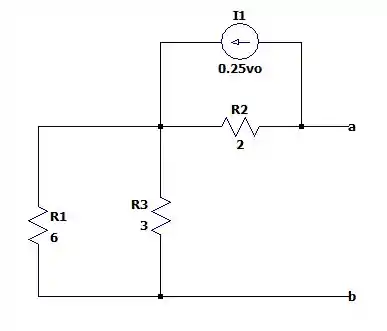
Fazendo a resistência equivalente entre e teremos:
Passo 3
Aqui nós entramos no caso em que não podemos fazer nada além de conectar uma fonte de valor unitário nos terminais e para encontrar a resistência de Norton, pois vamos então colocar uma fonte de entre elas da seguinte forma.
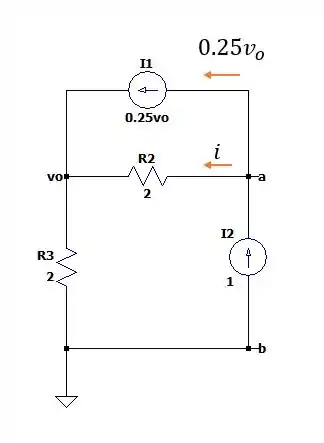
Aterrando e analisando todas as correntes que entram e saem no nó temos:
E agora analisando todas as correntes que que entram e saem no nó de tensão igual a teremos:
Dessa forma:
E substituindo esse valor na primeira equação nós encontraremos:
Isso nos dá a capacidade de saber a tensão no nó .
Então teremos a resistência de Norton ao fazer a divisão entre a tensão entre esses dois nós e a sua corrente: