Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 56
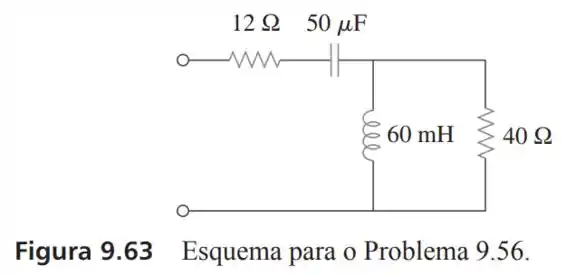
56- Com , determine a impedância de entrado do circuito mostrado na Figura .
Passo 1
Como foi dado o vamos calcular as impedâncias no capacitor e no indutor .
Passo 2
Dessa forma a impedância de entrada ou total será a impedância em paralelo do resistor de com o indutor e o equivalente entre eles somado com a resistência de e o capacitor, logo:
Quando trabalhar com fasores uses sempre valores exatos de módulo e de ângulo de fase na calculadora, pois muitos erros vão começar a aparecer a medida que você transforma fasor em número complexo e vice-versa
Resposta
Exercícios de Livros Relacionados
Calcule H ( s ) se a resposta é v . Use o resultado para calcular a resposta forçada, se v g = 5 cos tV .
Calcule H ( s ) se a resposta é (a) I 1 ( s ) , (b) I 0 ( s ) e (c) V 0 ( s ) .
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °
Calcule a impedância vista pelos terminais da fonte na Figura 10.4, nas formas retangular e polar.
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °