Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 36
Calcule a leitura do wattímetro
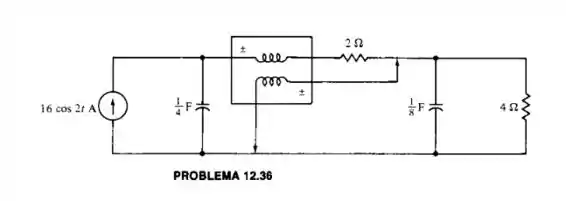
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, analisando a fonte de corrente, podemos perceber que a frequência é igual a
Com isso, podemos calcular os valores dos componentes no domínio da frequência
No caso, os resistores mantem a mesma resistência, por este motivo, já podemos calcular a resistência equivalente
E
Portanto, é igual a
Passo 2
Vamos supor que o nó que envolve o capacitor de 1/4 F, seja chamado , com isso, temos que é igual a
Que transformando para fasores, é igual a
Agora vamos pegar o ponto em que o wattímetro é conectado, vamos denominá-lo por , com isso, podemos calcular que é igual a
E a corrente
Passo 3
E podemos ir para potência nesse caso, que será a leitura do wattímetro
Substituindo os valores, nós temos que
Com isso, temos que
Logo, a leitura será de 32 W.