Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 43

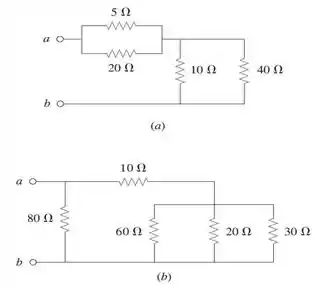
43. Calcule a resistência equivalente R a b nos terminais a - b para cada um dos circuitos da Figura 2.107.

Passo 1

Bora lá resolver um probleminha sobre associação de resistores:

a) Vamos analisar esse primeiro caso:

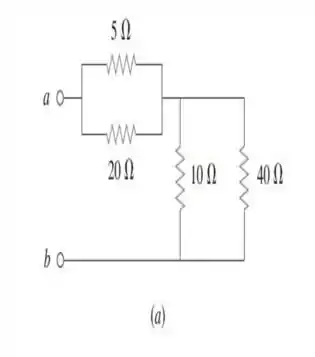
Vendo essa imagem, tiramos inicialmente que os resistores de 10   Ω e 40   Ω estão em paralelo. Calculemos a resistência equivalente para essa parte do circuito:

R e q 1 = ( 10 | | 40 )   Ω

R e q 1 = 10 ⋅ 40 10 + 40   Ω

R e q 1 = 8   Ω

E os resistores de 5   Ω e 20   Ω também estão em paralelo, de modo que a resistência equivalente R e q 2 vale:

R e q 2 = ( 5 | | 20 )   Ω

R e q 2 = 5 ⋅ 20 5 + 20   Ω

R e q 2 = 4   Ω

Essa R e q 1 está em série com a resistência R e q 2 . Desse modo, a resistência total equivalente R a b   é dada por:

R a b = R e q 1 + R e q 2

R a b = 8   Ω + 4   Ω

R a b = 12   Ω

Passo 2

b) Vamos analisar agora, esse segundo caso:

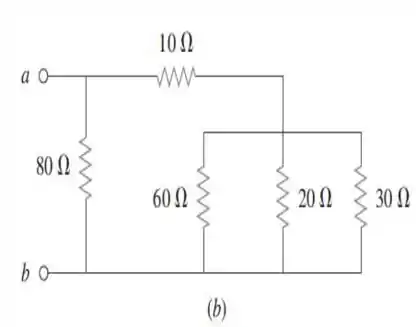
Nessa imagem podemos ver que os resistores de 60   Ω , 20   Ω e 30   Ω estão em paralelo. Assim, a resistência equivalente R e q 1 vai ser dada por:

R e q 1 = ( 60 | | 20 | | 30 )     Ω

1 R e q 1 = 1 60 + 1 20 + 1 30 Ω

1 R e q 1 = 1 + 3 + 2 60 Ω

6 R e q 1 = 60

R e q 1 = 60 6   Ω

R e q 1 = 10   Ω

Seguindo nosso raciocínio, podemos ver também que a resistências de R e q 1   e 10 Ω estão em série. A resistência proveniente dessa associação em série, está em paralelo com a resistência de 80   Ω ... Nesse caso, a resistência equivalente total R a b   vale:

R a b = ( 80 | | ( 10 + 10 ) )     Ω

R a b = 80 ⋅ 20 80 + 20 Ω

R a b = 1600 100 Ω

R a b = 16   Ω

Resposta

a)

R a b = 12   Ω

b)

R a b = 16   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se i 1 = 9 e i 2 = 6 na Fig. 2.17 (a) calcule a relação R 2 // R 1 .
Calcule a resistência equivalente, vista pela fonte, e use este resultado para encontrar i ,i 1ev .
Na Fig. 2.18, se N = 3, R 1 = 9 Ω ,R 2 = 72 Ω , e v = 12 s e ntV e o valor da potência instantânea entregue pela fonte de corrente é 24 s e n 2 tW , calcule (a) R 3 , (b) i e (c) i 3
Calcule a resistência equivalente vista pela fonte e a corrente i .
Calcule i 1 e i 2 .