Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 44
44- Determine a potência complexa liberada por para o circuito da Figura . Seja .
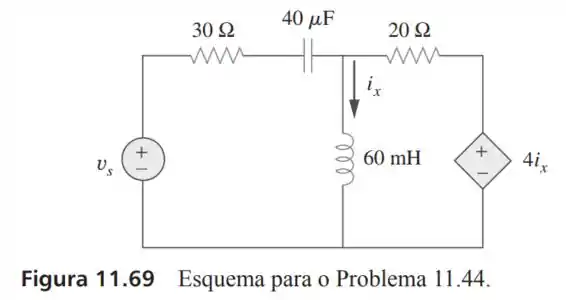
Passo 1
Sabendo que a fonte não é uma fonte então a potência liberada por ela terá valor igual a:
Onde
E que ela excita o circuito com uma velocidade angular igual a:
Então as reatâncias nos capacitores e indutores serão iguais a:
Passo 2
Isso nos dá então o seguinte circuito
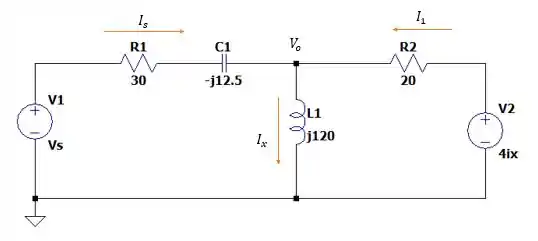
Fazendo a somatória das correntes que entram no nó temos:
Ou seja:
Essa conta nos dá:
Passo 3
Agora podemos encontrar substituindo , ou seja:
Então a potência complexa será:
Resposta
Exercícios de Livros Relacionados
As duas cargas mostradas na Figura P10.22 podem ser descritas da seguinte forma: a carga 1 absorve uma potência média de 10 kW e uma potência reativa de 4 kVAR; a carga 2 tem uma impedância de (60 + j
Suponha que o circuito da Figura P10.24 represente um circuito de distribuição residencial no qual as impedâncias dos condutores são desprezíveis e Vg1 = Vg2 = 110/0° V (ef). As três cargas no circuit
a) Determine VL (ef) e θ para o circuito da Figura P10.19, se a carga absorver 2.500 VA, com um fator de potência atrasado de 0,8. b) Construa um diagrama fasorial de cada solução obtida em (a).
Os valores dos parâmetros do circuito da Figura P10.56 são L 1 = 8m H ; L 2 = 2m H ; k = 0,75 ; R g = 1Ω e R L = 7Ω . Se v g = 54 2 cos 1000 tV , determinea) o valor eficaz de v o ;b) a potência méd