Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 46

46. Determine I no circuito da Figura 2.110 .

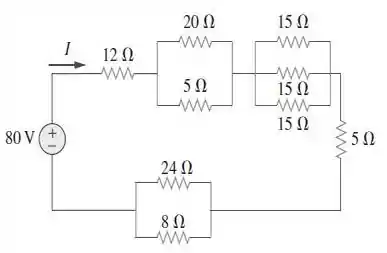
Passo 1

Bora lá resolver um probleminha sobre associação de resistores:

Vamos analisar direitinho esse circuito.

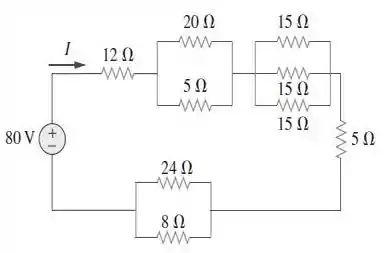
Vendo essa imagem, tiramos inicialmente que os resistores de 20 Ω e 5 Ω estão em paralelo. Calculemos a resistência equivalente para essa parte do circuito:

R_e q 1 = ( 20 | | 5 ) Ω

R_e q 1 = (20 * 5)/(20 + 5) Ω

R_e q 1 = 4 Ω

2 4 Ω está em paralelo com 8 Ω . Desse modo, a resistência equivalente R_e q 2 para esse trecho, é dada por:

R_e q 2 = [ 24 | | 8 ] Ω

R_e q 2 = (24 * 8)/(24 + 8) Ω

R_e q 2 = 6 Ω

Em seguida, podemos ver também ali três resistências de 15 Ω em paralelo, o que nos fornece uma resistência R_e q 3 igual a:

R_e q 3 = ( 15 | | 15 | | 15 ) Ω

(1)/(R_e q 3) = ((1)/(15) + (1)/(15) + (1)/(15)) Ω

(1)/(R_e q 3) = (1)/(5) Ω

R_e q 3 = 5 Ω

Agora não tem mais nada em paralelo. Tá tudo em série. Basta apenas pegar as resistências que obtivemos anteriormente e juntar com a de 12 Ω e 5 Ω para obter a resistência total R_T :

R_T = 12 Ω + 5 Ω + R_e q 3 + R_e q 2 + R_e q 1

R_T = 12 Ω + 5 Ω + 5 Ω + 6 Ω + 4 Ω

R_T = 32 Ω

Passo 2

Por fim, para obter a corrente I , basta dividir a fonte de tensão U presente pela resistência total R_T :

I = (U)/(R_T)

I = (80 V)/(32 Ω)

I = 2,5 A

Resposta

I = 2,5 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Y à direita ( 25 ; 37,5e125Ω ) por seu Δ equivalente.
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Y à esquerda ( 25 ; 40e100Ω ) por seu Δ equivalente.
Uma tela touch resistiva tem 640 pixels na direção x e 1.024 pixels na direção y. A malha resistiva tem 8 V aplicados em ambos os sentidos, x e y. As coordenadas de pixel no ponto de toque são (480, 1
72 a) Usando a Figura 3.38, deduza a expressão para a tensão vy.b) Supondo que haja py pixels na direção y, deduza a expressão para a coordenada y do ponto de toque, usando o resultado de (a).
Suponha que a tela sensível ao toque descrita no Problema 3.74 é tocada simultaneamente em dois pontos, um com coordenadas (480, 192) e outro com coordenadas (240, 384). a) Calcule a tensão medida nas