Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 36
36. Determine e no circuito da Figura
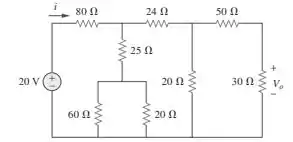
Passo 1
A primeira coisa que nós vamos fazer aqui é simplificar o máximo o nosso circuito e uma coisa que não sei se você está vendo, mas existem dois resistores em paralelos aqui...
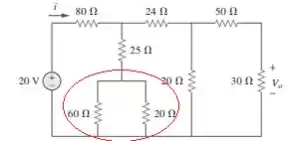
Dois resistores em paralelos podem ser substituídos por um resistor equivalente () fazendo a regra do produto pela soma...
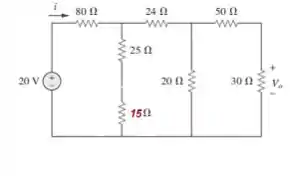
Agora perceba que resistor de está em série com o de gerando como resultado...
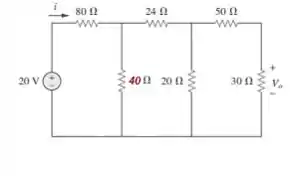
Infelizmente não dá mais para simplificar mais . Cuidado! Muitos tendem a achar que o resistor e o de estão em paralelos o que não é verdade, já que temos um resistor de entre eles.
Passo 2
Com o circuito simplificado ao máximo (sem perder nenhuma parte importante como o resistor de ), chegou a hora de buscarmos a corrente que o circuito está demandando. Vamos nessa?
Podemos aplicar aqui a lei de Kirchoff para as tensões (lei das malhas):
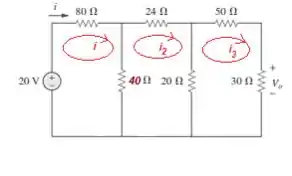
Aplicando então a lei das malhas em cada uma dessas três malhas...
Passo 3
A partir de agora vamos começar a simplificar essas três equações:
- Primeiro vamos eliminar os parênteses de todo mundo...
Juntando os temos semelhantes agora...
Isolando o na equação de cima (equação )...
Substituindo esse resultado nas duas equações de baixo (equações () e ):
Simplificando esse sistema...
Multiplicando a equação de cima por ...
Somando essas duas equações...
Prontinho! Achamos a corrente :
Passo 4
Podemos agora encontrar a tensão , sabendo qual é a corrente (a corrente que passa pelo resistor). É bem tranquilo fazer isso já que no passo anterior descobrimos o valor de e, além disso, descobrimos esse valor através do sistema...
Jogando a informação de na equação :
Beleza, então, de acordo com a Lei de Ohm...
Como ...