50. Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor a transformação de fontes.
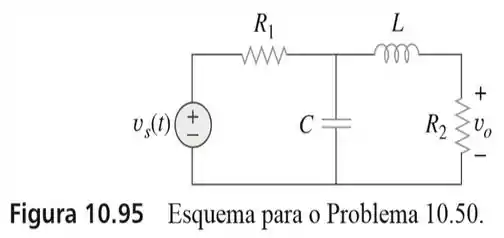
Passo 1
Fala galerinha! Como é um problema que nós mesmos vamos ter que elaborar, bora redesenhar esse circuito atribuindo valores pros seus elementos.
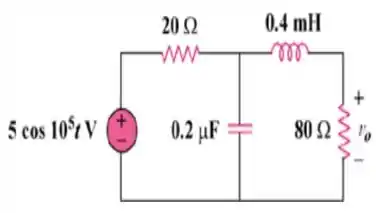
E depois, bora passar os elementos pro domínio da frequência:
Só que essa associação em série entre a fonte de tensão e a resistência de , pode ser transformada em uma associação em paralelo entre a mesma resistência, e uma fonte de corrente dada pela divisão da tensão pela resistência:
Passo 2
E o nosso circuito fica do seguinte jeito:
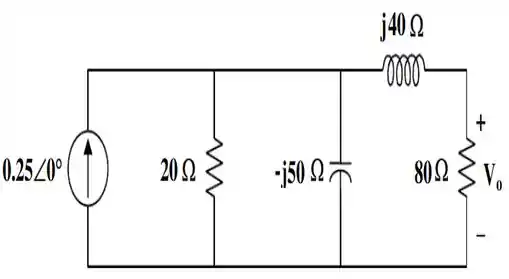
O resistor de e o capacitor de estão em série. Desse modo, a impedância equivalente para essa parte do circuito vai valer:
E a tensão para essa parte do circuito vai ser dada pelo produto da impedância pela corrente corrente de :
Passo 3
Mas por que nós fizemos isso? Ora bolas, a associação em paralelo entre a fonte de corrente e a impedância , composta pelo resistor e indutor; vai virar uma associação em série entre a mesma impedância e a fonte de tensão , que acabamos de descobrir. Sendo assim...
Nosso circuito, pode ser remodelado para o seguinte jeito:
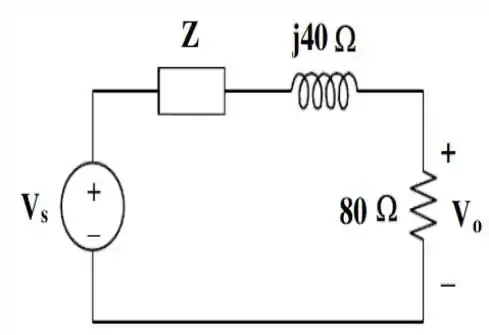
Por divisão de tensão, obtemos que o valor de é dado por:
Passando para o domínio do tempo:
E voilà! Encontramos nossa resposta!