Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 58
58- A rede na Figura representa um modelo de um amplificador com transistor bipolar de emissor comum conectado a uma carga. Determine a resistência de Thévenin vista pela carga.
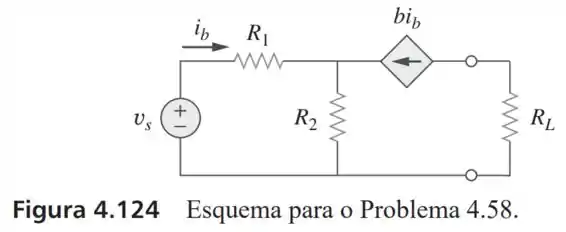
Passo 1
Vamos retirar a carga e ver o que temos:
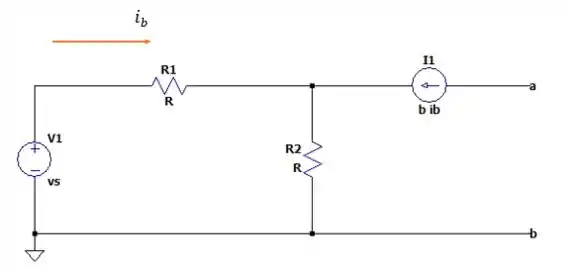
Se desaterrarmos o circuito nós encontraremos a seguinte relação:
Fechando esse circuito conseguiremos encontrar a corrente de Norton.
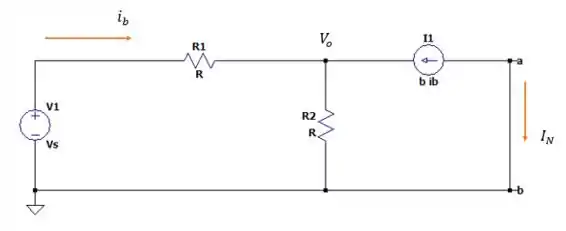
Fazendo a somatória das correntes no nó teremos:
Agora correlacionando com teremos:
Isolando teremos:
Agora fazendo a somatória das correntes no nó vemos que:
Ou seja:
Passo 2
Agora note que não há como especificarmos o valor de ou seja o valor de pois não há uma resistência entre esse ponto e o ponto de tensão igual a , que é onde se encontra a tensão de corrente, havendo um curto nessa região ou seja:
Por consequência , a carga deveria ser ligada nesse ponto (que é onde é feito nos transistores) e não entre e . Então somente teremos como resposta a corrente de Norton.