Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 50
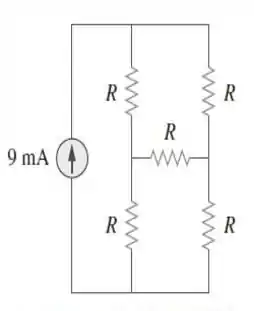
50. Elabore um problema para ajudar outros estudantes a entender melhor as transformações usando a Figura 2.114.
Passo 1
Bom! Como estamos trabalhando com corrente e resistência, uma boa pedida seria que o nosso problema envolvesse potência, já que a fórmula da potência é o produto da resistência equivalente pela corrente ao quadrado, .
Então, o nosso problema vai ser o seguinte:
Qual valor de no circuito da Fig. faria com que a fonte de corrente entreguasse aos resistores?
É isso que vamos descobrir!
Olhá só! Tem uma parte do nosso circuito que se assemelha muito a uma configuração em estrela! Ela está destacada na figura abaixo:
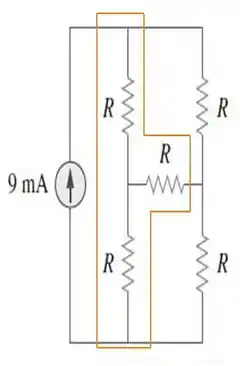
E essa parte destacada realmente condiz de fato, com uma configuração estrela. Só que para esse caso específico não é legal trabalhar com o formato estrela, mas sim com o formato delta. Por isso, vamos usar a transformação de em :
Para fazer isso, basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Onde o que nos leva ao seguinte resultado:
Passo 2
Obtemos assim, o seguinte circuito:
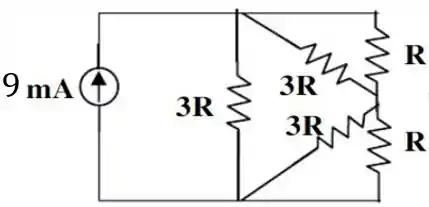
Nesse circuito, dá pra perceber que as resistências de e estão em paralelo tanto na parte de cima quanto de baixo. Ou seja, estão duplamente paralelas.
Calculemos então o valor da resistência equivalente dessa associação em paralelo:
Só que como já mencionamos, tem outra associação em paraelo entre e ... De modo que a resistência equivalente pra essa parte do circuito vale:
E o nosso circuito fica do seguinte jeito:
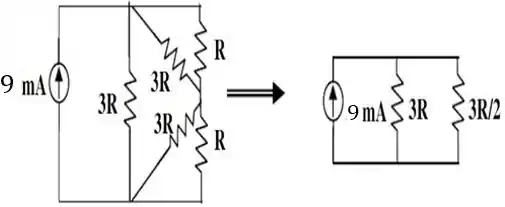
Com isso, vemos que a resistência equivalente total do circuito vai ser dada pela associação em paralelo entre e :
Passo 3
Finalmente, sabendo que a potência, , é dada por:
Como determinamos que vale e sabemos que é igual a; só presisamos determinar o valor de . Vamos lá, então: