Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 65
65- Para o circuito mostrado na Figura , determine a relação entre e .
Passo 1
Vamos abrir o circuito de modo que tenhamos a carga em cinza no esquema do enunciado.
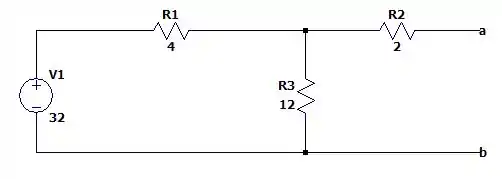
Como não aterramos nenhum dos dois terminais e com isso a fonte de não irá afetar em nada no circuito sendo uma linha contínua de modo que teremos a seguinte malha resistiva abaixo.
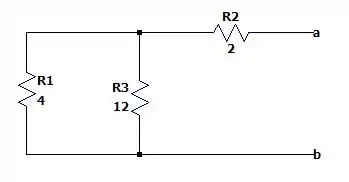
De forma que os resistores de e estão em paralelo e a associação desses dois resistores está em série com o resistor de , então a resistência de Norton será igual a:
Passo 2
Agora vamos fechar a conexão para calcular a corrente de Norton.
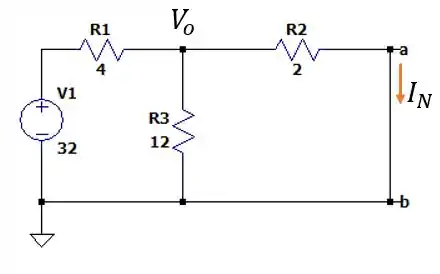
Mas antes de calcular essa corrente , vamos calcular a corrente total desse circuito todo. E para isso vamos notar que as resistências de e estão em paralelos e que a associação entre esses dois resistores está em série com o resistor de nos dando uma corrente total igual a:
E com isso a corrente total valerá:
Dessa forma o valor de será:
Então o valor de (pelo ponto de tensão igual a e será):
Com esse valor de corrente de Norton nós teremos o valor da tensão de Thévenin e ela será:
Passo 3
Então pelos parâmetros encontrados no passo anterior nós teremos duas fontes. E elas estão abaixo.
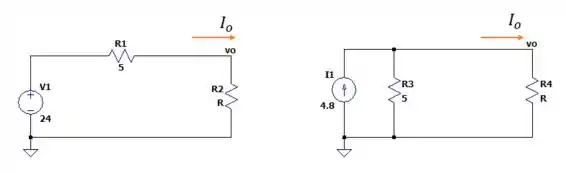
Pela primeira fonte nós temos:
Já a segunda fonte não nos dá nenhum resultado, até por que não temos nenhum valor de resistência para a carga, sendo necessário transformar para uma fonte de tensão, tal como na primeira.