Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas Abrangentes - Ex. 96
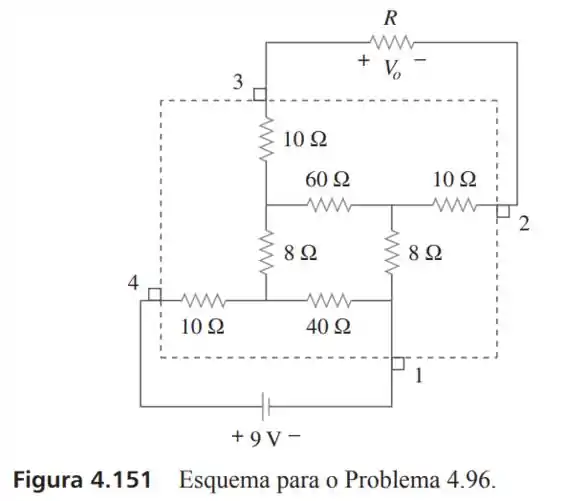
96- Um conjunto de resistências é conectado a um resistor de carga e uma bateria de conforme mostrado na Figura .
Determine o valor de tal que
Calcule o valor de que drenará a corrente máxima. Qual é a corrente máxima?
Passo 1
Vamos desenhar as correntes em cada malha de tal modo que não temos a carga conectada no circuito, para podermos calcular a tensão de Thévenin do circuito:
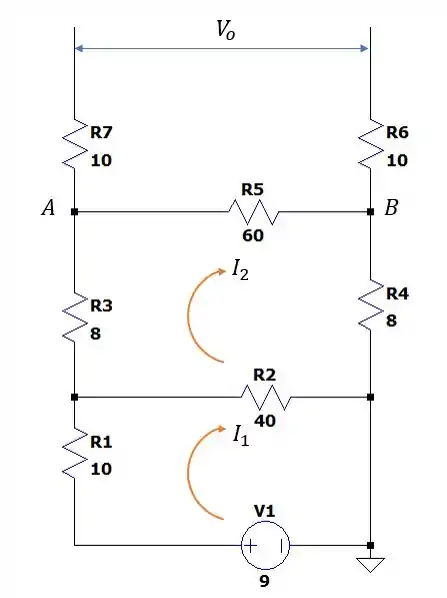
Da malha podemos tirar a seguinte somatória de tensões:
Da malha temos as seguintes tensões:
Logo:
E a tensão será igual a tensão entre os pontos e pois nenhuma corrente passa pelos resistores de , então:
Passo 2
Agora vamos calcular a resistência de Thévenin do circuito ao tirar a fonte:
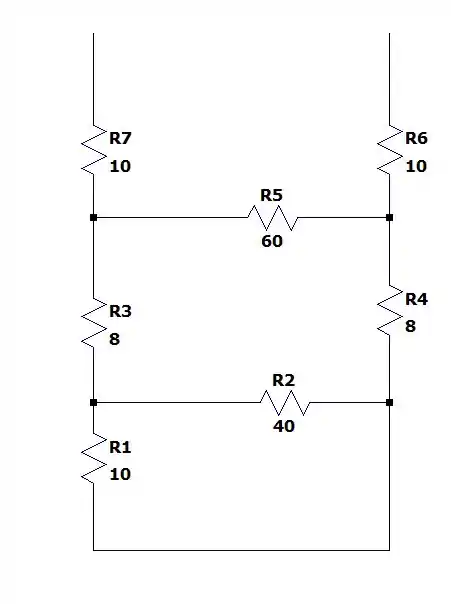
Começando pela resistência em paralelo entre e :
Deixando nosso circuito com:
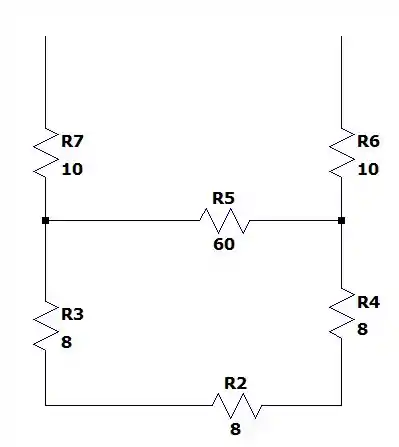
Três resistência de em série nos dando:
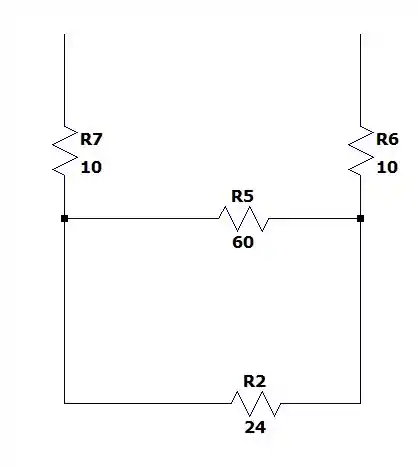
Com e em paralelo:
Logo a resistência entre os terminais será de:
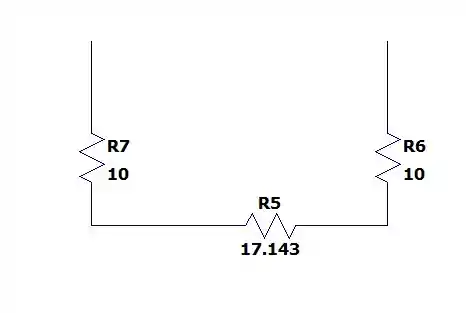
Passo 3
Então para a tensão nos terminais ser de nós devemos ter uma carga igual a:
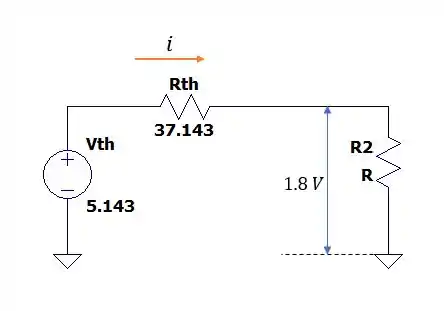
A relação entre as tensões pode ser entendida da seguinte forma:
Passo 4
A corrente no circuito da figura anterior será igual a:
Então quanto menor o valor de maior a corrente, ou seja: