Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 51b
51- Dado o circuito da Figura , obtenha o equivalente de Norton conforme visto dos terminais:
Passo 1
Tirando as fontes independentes temos a seguinte malha resistiva em volta dos contatos .
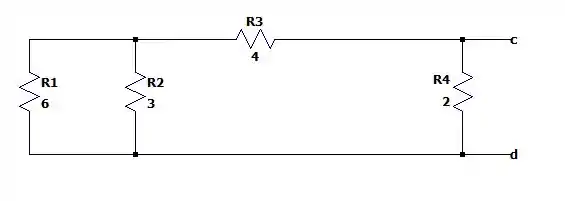
Sabendo que a resistência equivalente entre os resistores paralelos de e de dá nós teremos a seguinte malha equivalente:
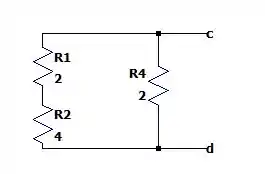
Então a resistência de Thévenin entre esses contatos será de:
Passo 2
Agora vamos voltar com as fontes e ver que se fecharmos o contato entre nenhuma corrente passará pelo resistor de de modo que tenhamos agora o seguinte circuito.
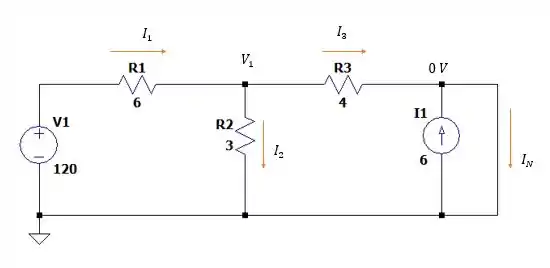
Uma vez que quando interligamos com o nó passa a ter uma tensão de .
Dessa forma a somatória das correntes no nó será de:
Dessa forma:
O que nos dá:
Passo 3
Então a corrente de Norton passa a valer:
Mesmo colocando tensão zero nos dois terminais da fonte de corrente ela ainda assim estará ligada e mandando corrente, só que somente na direção do curto circuito entende? Não é uma questão de segurança e sim de quanto de corrente vai passar naquela linha caso façamos isso.