Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 51
51. Use a transformação de fontes para determinar no circuito do problema
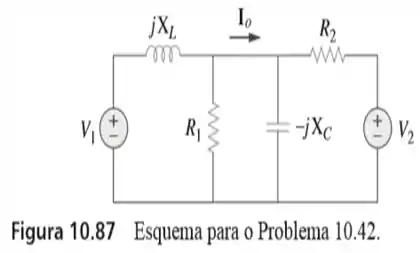
Passo 1
Olha só! Como é um problema que nós mesmos temos que elaborar... A primeira coisa a se fazer, é atribuir alguns valores aleatórios para os elementos desse circuito. Vamos lá!!
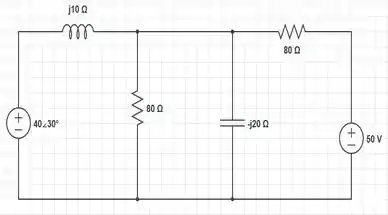
Nessa figura que esboçamos; há a presença nas extremidades esquerda e direita, de uma fonte de tensão e de uma impedância em série, seja um indutor ou um resistor.
O que precisamos fazer pra esse caso, é usar a transformação de fontes, para converter a associação em série da fonte de tensão, com o indutor ou resistor em uma associação em paralelo entre uma fonte de corrente e as mesmas impedâncias.
Passo 2
Vamos então, calcular o valor das correntes:
Para a extremidade esquerda...
Para a extremidade direita...
Olha só! Com isso, passaremos a ter dois resistores de em paralelo, cuja resistência equivalente vai valer metade disso, ou seja . O ponto aqui é outro.
Antes tínhamos uma corrente de circulando em um resistor de . Como o outro resistor é de , também vai circular nele uma corrente de . Desse modo, a corrente total circulante é de .
Sendo assim, nosso circuito passa a ter a seguinte aparência:
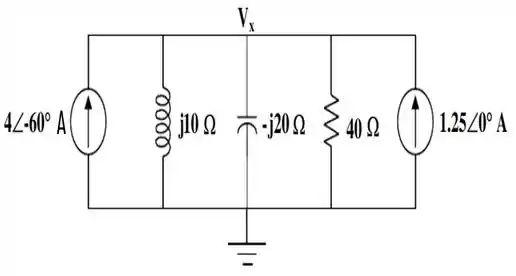
E a tensão é dada facilmente, por:
Passo 3
Mas nós queremos na verdade, é o valor de .
Bom! Por análise nodal, olhando a figura do enunciado e do , sabemos que é dada por:
Substituindo ...
Finalmente obtemos nossa resposta!