Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 2
Use a análise nodal para calcular o valor de em regime permanente, se e calcule a amplitude de para os casos de (a) , (b) e (c) rad/s. Compare o resultado para este circuito com o da Fig. 11.6.
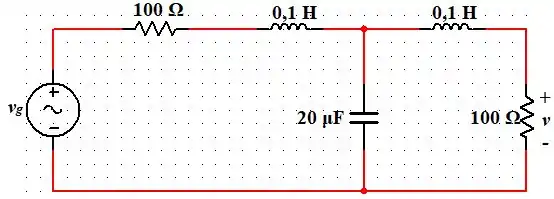
Passo 1
Falaee!! Seguinte... Vamos para o primeiro caso (a), em que . A gente sabe que as reatâncias capacitiva e indutiva são dadas da seguinte forma:
A gente percebe de forma bem simples que ao fazer tender a 0 nessas fórmulas aí de cima, vemos que e . Oooou seja, é como se o capacitor tivesse uma capacitância enoooorme (dando a entender um circuito aberto) e o indutor não tivesse indutância nenhuma (dando a entender um circuito fechado). Dessa forma, teríamos o seguinte circuito equivalente:
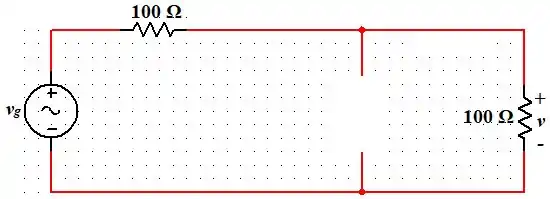
Agora ficou fácil perceber que, como os resistores são iguais a queda de tensão é dada por:
Logo, a amplitude é dada por:
Muito simples essa né? ;)
Passo 2
Para o caso (b), temos que rad/s. Assim, substituindo o circuito dado pelos valores das reatâncias indutivas e capacitivas (mostrado pelas fórmulas apresentadas anteriormente) atribuindo o valor de rad/s. Temos que:
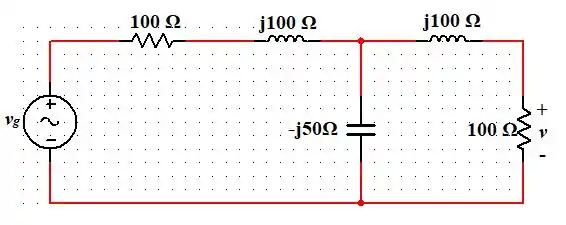
Agora, vamos selecionar o seguinte nó e atribuir direções da corrente e também vamos colocar o terra (referencial de potencial 0 V) na parte de baixo do circuito para facilitar nossa vida hehe:
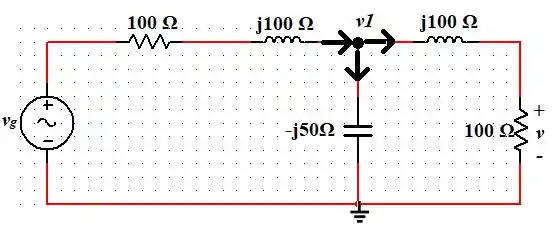
Dessa forma, utilizando a Lei dos Kirchhoff das Correntes no nó , temos:
Ainda, pelo circuito acima percebemos que:
Agora é só resolver esse sistema hehe:
Resolvendo o sistema pela Regra de Cramer para o sistema 2x2, temos que é:
Portanto, podemos analisar que a amplitude nesse caso é dada por .
Passo 3
Para o caso (c), temos que rad/s. Assim, substituindo o circuito dado pelos valores das reatâncias indutivas e capacitivas (mostrado pelas fórmulas apresentadas anteriormente) atribuindo o valor de rad/s. Temos que:
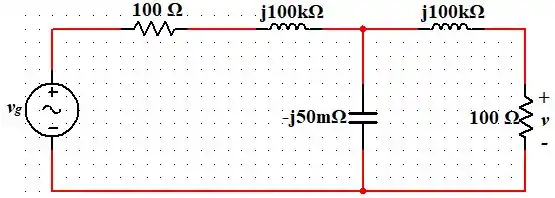
Agora, vamos selecionar o seguinte nó e atribuir direções da corrente e também vamos colocar o terra (referencial de potencial 0 V) na parte de baixo do circuito para facilitar nossa vida hehe:
Dessa forma, utilizando a Lei dos Kirchhoff das Correntes no nó , temos:
Ainda, pelo circuito acima percebemos que:
Agora é só resolver esse sistema:
Resolvendo o sistema pela Regra de Cramer para o sistema 2x2, temos que é:
Portanto, podemos analisar que a amplitude nesse caso é dada por .
Resposta
a)
b)
c)