Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 55

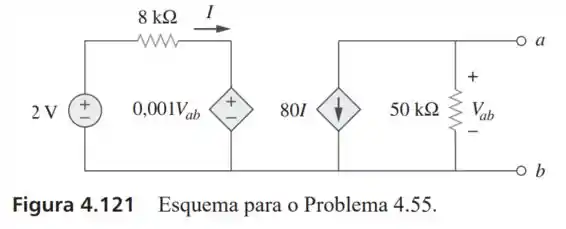
55- Obtenha o equivalente de Norton nos terminais a - b do circuito da Figura 4.121 .

Passo 1

Vamos repetir o que fizemos na questão anterior (já que calculamos todas as correntes de fonte equivalente) pois a idéia será a mesma.

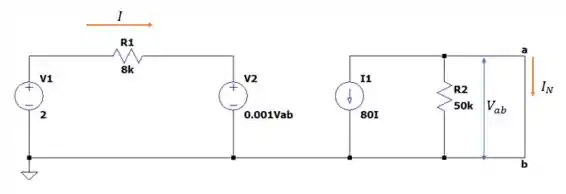
Vamos dar inicio a nossa questão aplicando Lei de tensão de kirchhoff ao circuito pelo lado esquerdo.

8 × 10 3 I + 0.001 V a b = 0

8 × 10 3 I = - 0.001 V a b

I = - 0.001 8 k =

I = - 0.125   m A V a b

Passo 2

Vamos aplicar agora a Lei das Correntes de Kirchhoff no nó V a b

I = 80 I + V a b 50 × 10 3               ( 1 )

Substituindo I   na expressão, temos:

I = 80 - 0.125 × 10 - 6 V a b + V a b 50 × 10 3

I = - 0.5 V a b + V a b 50 × 10 3

50 × 10 3 = 0.5 V a b

Logo

V a b = 100 × 10 3 V

Passo 3

Portanto, a resistência de Norton é

R N = V a b i o

= 100 × 10 3 1

R N = 100 × 10 3

Portanto, o valor da resistência de Norton R N = 100   k Ω .

Passo 4

Já para calcular a tensão de Thévenin V a b = V t h vamos considerar o circuito aberto em a - b .

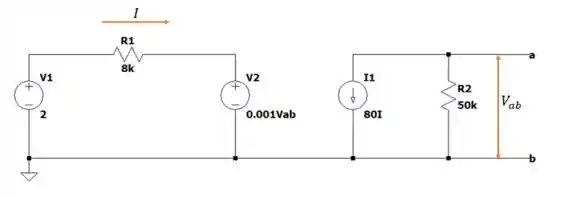
Partindo do circuito acima

V a b = 0 V   ( c u r t o - c i r c u i t o )

Aplicando a Lei de Tensão de Kirchhoff ao circuito do lado esquerdo

- 2 + 8 × 10 3 I + 0.001 V a b = 0

- 2 + ( 8 × 10 3 ) I + 0.001 ( 0 ) = 0

- 2 + ( 8 × 10 3 )   I + 0 = 0

8 × 10 3 I = 2

I = 2 8 × 10 3

I = 0.25 × 10 - 3

Portanto, o I   atual e de 0.25   m A .

Passo 5

Vamos aplicar a Lei das Correntes de Kirchhoff no nó V a b

80 I + V a b 50 × 10 3 + i s c = 0

80 I + 0 50 × 10 3 + i s c = 0

80 I + 0 + i s c = 0

i s c = - 80 I           ( 2 )

Substituindo o novo valor de I , iremos obter:

i s c = - 80 ( 0.25 × 10 - 3 )

i s c = - 20 × 10 - 3

Portanto, a corrente de Norton é de i s c = I N = - 20   m A

( O B S = i s c = i c u r t o - c i r c u i t o ,   ,   l o g o   s c   s i g n i f i c a   s h o r t - c i r c u i t )

Passo 6

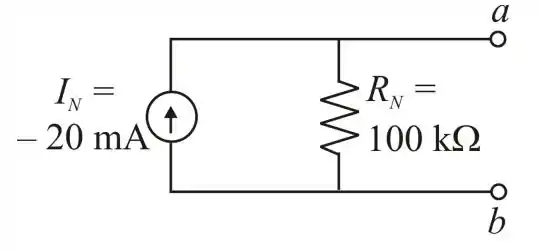
Logo o circuito equivalente de Norton é mostrado na imagem a seguir.

Resposta

I N = - 20   m A

R N = 100   k Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

86- Uma caixa preta com um circuito nela embutido é conectada a um resistor variável. São usados um amperímetro ideal (com resistência zero) e um voltímetro ideal (com resistência infinita) para medir
87- É feito o modelo de um transdutor com uma fonte de corrente I s e uma resistência em paralelo R s . A medição da corrente nos terminais da fonte resulta em 9.975m A quando for usado um amperímetro
91- ( a ) Na ponte de Wheatstone da Figura 4.147 , selecione os valores de R 1 e R 3 , tais que a ponte possa medir R x no intervalo de 0Ω a 10Ω . ( b ) Repita o exercício para um intervalo de 0Ω a 10
92- Considere a ponte da Figura 4.148 . A ponte se encontra equilibrada? Se o resistor de 10k Ω for substituído por um resistor de 18k Ω , que resistor conectado entre os terminais absorve a potência
93- O circuito da Figura 4.149 é um modelo de amplificador com transistores de emissor comum. Determine i x usando transformações de fontes.