Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 57
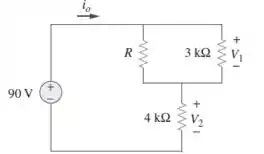
57. No circuito da Figura 3.102, determine os valores de R, V1
e V2 dado que io = 15 mA.
Passo 1
A corrente é a mesma corrente que passa pelo resistor de , porque a corrente vai se dividir nos resistores e , e se juntar novamente quando estiver saindo deles:
Agora nós podemos somar as quedas de tensão do circuito:
Sabemos o valor de :
Passo 2
A única coisa que falta descobrir agora é o valor da resistência . Vamos dizer que a corrente que passa pelo resistor R é e a corrente que passa pelo resistor de é .
Pela lei de Ohm a gente sabe que:
Então precisamos descobrir o valor da corrente , pela lei de Kirchhoff:
E a corrente é fácil de achar, só usar a lei de Ohm:
Então a corrente vale:
Então é só usar a Lei de Ohm mais uma vez e terminamos o exercício:
Resposta
Exercícios de Livros Relacionados
33. Qual dos circuitos da figura 3.82 é planar? Para o circuito planar, redesenhe os circuitos para que não existam ramos cruzando entre si.
34. Determine qual dos circuitos da Figura 3.83 é planar e redesenhe-o de modo a que não apresente ramos cruzados.
35. Resolva o problema 3.5 , usando análise de malhas.
36. Use a análise de malhas para determinar i 1 , i 2 e i 3 no circuito da figura 3.84 .
a) Use o método das correntes de malha para determinar as correntes de ramo i a - i e no circuito da Figura P4.52.b) Verifique sua solução mostrando que a potência total gerada no circuito é igual à p