Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 60
60- Para o circuito da Figura , determine e o fator de potência de entrada.
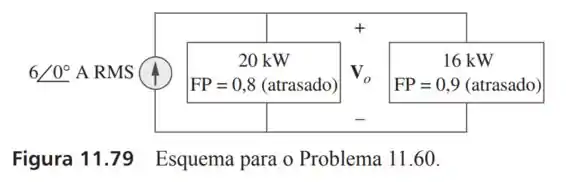
Passo 1
Vamos encontrar a potência total das duas cargas do sistema, sabendo que o fator de potência atrasado representa uma reatância indutiva:
Começando pela carga com fator de potência igual a
E agora para a outra carga:
Passo 2
Agora somando as duas potências nós teremos:
Dessa forma a potência que é a mesma nas duas cargas será igual a:
Passo 3
E o fator de potência será:
Como o ângulo é positivo, nós teremos uma carga indutiva, portanto o fator de potência é atrasado.
Resposta
Exercícios de Livros Relacionados
54- Para o circuito da Figura 11.73 , determine a potência complexa absorvida por cada elemento.
59- Calcule a potência reativa no indutor e no capacitor da Figura 11.78
53- No circuito da Figura 11.72 , a carga A recebe 4k V A com F P = 0.8 (adiantado). A carga B recebe 2.4k V A com F P = 0.6 (atraso). C é uma carga indutiva que consome 1k W e recebe 500V A R . ( a )
56- Obtenha a potência complexa liberada pela fonte no circuito da Figura 11.75