Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 68
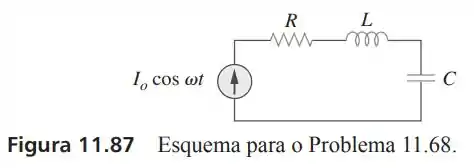
68- Calcule a potência complexa fornecida pela fonte de corrente no circuito em série da Figura
Passo 1
A corrente não está em pois foi nos dada a amplitude máxima então:
E a impedância total desse circuito será:
Uma vez que a reatância capacitiva é sempre negativa e a indutiva sempre positiva.
Passo 2
A potência total pode ser calculada por:
Logo a potência complexa (deixando a impedância na sua forma complexa mesmo) será:
Resposta
Exercícios de Livros Relacionados
Prove que, se apenas o módulo da impedância de uma carga puder variar, a maior potência média lhe será transferida quando Z L = | Z t h | . [Sugestão: ao deduzir a expressão para a potência média da c
a) Determine a potência média dissipada em cada resistor no circuito da Figura P10.39.b) Confirme sua resposta demonstrando que a potência total fornecida é igual à potência total absorvida.
O fasor tensão V a b , no circuito da Figura P10.43, é 300 ∠ 0 °V ( e f ) , quando nenhuma carga externa está ligada aos terminais a, b. Quando uma carga de impedância 200 - j 500Ω é ligada aos termin
a) Determine a potência média dissipada na linha na Figura P10.31.b) Determine a reatância capacitiva que, quando ligada em paralelo com a carga, fará com que esta se comporte como uma carga puramente
O resistor variável no circuito da Figura P10.46 é ajustado até que a potência média que ele absorve seja máxima.a) Determine R.b) Determine a máxima potência média.c) Encontre um resistor no Apêndice