Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 56
56- Obtenha a potência complexa liberada pela fonte no circuito da Figura
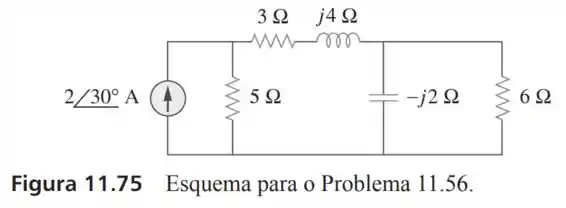
Passo 1
A impedância equivalente desse circuito será:
Segue o flow:
A resistência de está em paralelo com a reatância de , que por sua vez essa equivalência está em série com a impedância de e toda essa resistência está em paralelo com a resistência de . Nos dando a conta bonitinha a fazer em cima.
Passo 2
Então a potência aparente será calculada por:
Sempre quando está escrito “potência liberada pela fonte”, entende-se que a fonte está em .
Então:
Resposta
Exercícios de Livros Relacionados
49- Determine a potência complexa para os seguintes casos: d ) V R M S = 120 ∠ 30 °V ,Z = 40 + j 60Ω
42- Uma fonte de 110VR M S ,60H z é aplicada a uma impedância de carga Z . A potência aparente entrando na carga é de 120V A com um fator de potência 0.707 atrasado. ( a ) Calcule a potência complexa
44- Determine a potência complexa liberada por v s para o circuito da Figura 11.69 . Seja v s = 100 cos 2000 tV .
58- Obtenha a potência complexa liberada para o resistor de 10k Ω da Figura 11.77 a seguir.
62- Para o circuito da Figura 11.81 , determine V s .