Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 62
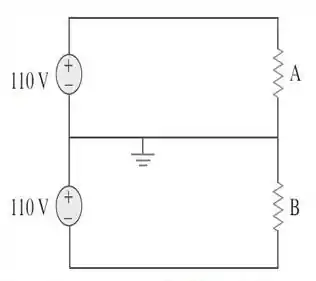
62. Um sistema trifásico alimenta duas cargas e , conforme mostrado na Figura . A carga é formada por um motor que drena uma corrente de , enquanto a carga é um que consome . Considerando de uso por e , calcule o custo anual de consumo de energia do sistema.
Passo 1
Olha que beleza! Que questãozinha mais sussa! Sabe por quê?
É só o basicão de circuitos elétricos! A fórmula da potência é dada simplesmente pelo produto da fonte de tensão pela fonte de corrente circulante.
E pra nossa felicidade já temos tudo o que precisamos.
Só precisamos calcular a potência separadamente para cada parte e depois somar tudo usando as fórmula abaixo:
A corrente , do enunciado tiramos que vale e a corrente vai valer . Sendo assim, basta fazer os cálculos:
E somando tudo, obtemos a potência total:
Passo 2
Por fim, para obter o custo anual, basta utilizar a fórmula abaixo:
Bom! O número de dias, como a questão pede o consumo anual; é . E quanto a potência, nós já obtivemos anteriormente. Só temos que ter o cuidado de dividir por , já que estamos trabalhando com .
O resto das coisa já temos em mãos. Bora fazer o cálculo: