Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 63

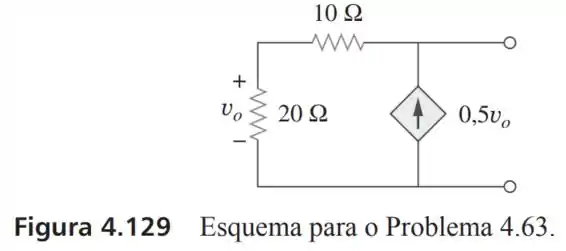
63- Determine o equivalente de Norton para o circuito da Figura 4.129 .

Passo 1

Vamos fechar os dois contatos abertos para encontrar a corrente de Norton.

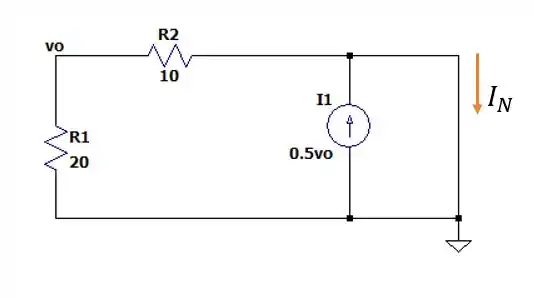
Aterrando o terminal de baixo nós podemos considerar que toda a corrente que seria gerada pela fonte dependente iria para a linha onde passa a corrente I N ou seja:

I N = 0.5 v o

Só que se nenhuma corrente passa pelos dois resistores então nenhuma tensão é gerada no resistor de 20   Ω então:

v o = 0

Se v o = 0 logo:

I N = 0   A  

Consequentemente então:

V t h = 0   V

Passo 2

Porém isso não diz que não há nenhuma resistência entre esses terminais e isso que nós veremos:

A melhor forma de encontrar a resistência equivalente do circuito e a melhor forma é conectar esse terminal a uma fonte de 1   V , isso nos dá o seguinte circuito.

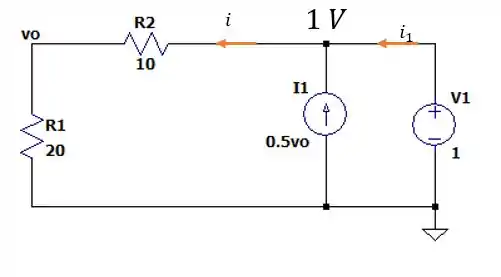
Pelo nó de 1   V acima da fonte dependente de corrente temos que:

1 - v o = 10 i

E pelo nó v o temos:

v 0 = 20 i

Dessa forma:

1 - 20 i = 10 i → i = 1 30

E:

v o = 20 30 = 2 3   V

Passo 3

Então o valor da corrente i 1 que a fonte de 1   V libera vale:

i = 0.5 v o + i 1

i 1 = i - 0.5 v o = 1 30 - 0.5 × 2 3 = - 0.3   A

Dessa forma o valor de R N será calculado dividindo a tensão pela corrente da fonte que colocamos ali naquele ramo e ela será de:

R N = V I = 1 - 0.3 = - 3.333   Ω

Resposta

I N = 0   A

R N = - 3.333   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A ponte de Wheatstone, no circuito da Figura P4.73, está equilibrada quando R3 é igual a 3000Ω . Se o galvanômetro tiver uma resistência de 50 V, qual será a corrente no galvanômetro quando a ponte es
Obtenha o equivalente de Norton em relação aos terminais a, b do circuito da Figura P4.81.
Um voltímetro com uma resistência de 85,5 kV é usado para medir a tensão V a b no circuito da Figura P4.72.a) Qual é a leitura do voltímetro?b) Qual será a percentagem de erro na leitura do voltímetro
Obtenha o equivalente de Thévenin em relação aos terminais a, b do circuito da Figura P4.80.
Qual percentagem da potência total gerada no circuito da Figura P4.82 é fornecida a R 0 quando R 0 é ajustado para a máxima transferência de potência?