Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 64

64- Determine I s no circuito da Figura 11.83 , se a fonte de tensão fornece 2.5   k W e 0.4   k V A R (adiantado)

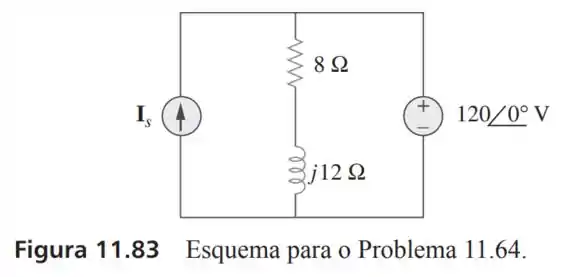
Passo 1

A corrente que flui na carga de 8 + j 12 Ω é igual a corrente que sai da fonte de corrente com a corrente que sai da fonte de tensão.

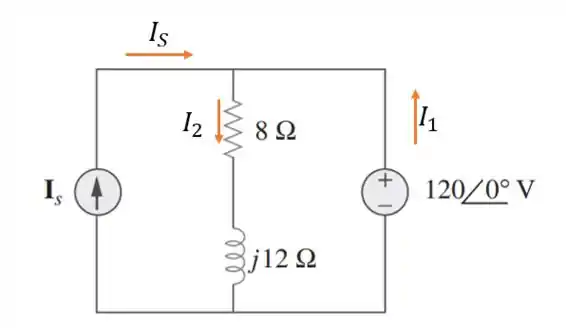
Como a fonte de corrente não altera a tensão nas impedâncias de 8 + j 12 então a corrente I 2 que passa por elas será de:

I 2 = 120 ∠ 0 8 + j 12 = 120 ∠ 0 14.42 ∠ 56.31 ° = 8.32 ∠ - 56.31   A

Passo 2

E como foi nos dado a potência que a fonte libera então:

S = 2.5 - j 0.4 k V A = 2.53 ∠ - 9.09   k V A

Então I 1 será calculado por:

I 1 * = S V = 2.53 ∠ - 9.09   k V A 120 ∠ 0 = 21.08 ∠ - 9.09   A =

Ou seja:

I 1 = 21.08 ∠ 9.09   A

Passo 3

Então pela somatória das correntes que entram no nó temos:

I S + I 1 = I 2

I S = I 2 - I 1 = 8.32 ∠ - 56.31 - 21.08 ∠ 9.09

I S = ( 8.32 cos ⁡ - 56.31 - 21.08 cos ⁡ 9.09 ) + j ( 8.32 sin ⁡ - 56.31 - 21.08 sin ⁡ 9.09 )

I S = - 16.2 - j 10.256 = 19.17 ∠ - 147.66 °   A

Lembrando que por tanto a parte real tanto a imaginária serem negativas então nossa fasor estará no terceiro quadrante. Tendo então que ter uma capricho especial na hora de fazer.

E como transformamos algumas vezes de fasor para número complexo e vice-versa nós acabamos tendo mais chances de aumentar nossa porcentagem de erro, então use com sabedoria essa transformação.

Resposta

I S = - 16.2 - j 10.256 = 19.17 ∠ - 147.66 °   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o valor eficaz da corrente em regime permanente através de resistor de 2 ⋅ Ω , se v r = 3 c o s ⁡ tV
Calcule o valor eficaz da corrente i em regime permanente e o fator de potência visto pelos terminais da fonte. Que elementos deve-se conectar em paralelo com a fonte para corrigir o fator de potência
Calcule o valor eficaz da corrente em regime permanente sobre o resistor de + Ω .
Calcule a potência media absorvida pelo capacitor, os dois resistores e a fonte.
Para um capacitor de C farads, conduzindo uma corrente i = I m c o s ⁡ ( ω t ) , verifique por (12.6) que a potência média é zero. Repita para um indutor de L henrys.