Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 23

Calcule o valor eficaz da corrente em regime permanente através de resistor de 2 ⋅ Ω , se v r = 3 c o s ⁡ t   V

Passo 1

Fala aí pessoal tudo belezinha? O enunciado pede que a gente determine valor eficaz da corrente em regime permanente através de resistor de 2 ⋅ Ω , se v r = 3 c o s ⁡ t   V .

V g = 3 a r s ⁡ t V

3 - v 1 3 = - v 1 j + v 1 2 + v 1 - v 6 ⇒ 6 - 2 v 1 6 = - 6 v 1 + j v 1 - j v + 4 j v 1 6 j ⇒

⇒ 6 j - 2 j v 1 = - j v + v 1 ( - 6 + 5 j ) ⇒ - j v + v 1 ( - 6 + 7 j ) = 6 j

v 1 - V 6 = V - 24 j ⇒ v 1 - V 16 = - v 424 j ⇒ 4 j v 1 - 4 j V = - V ⇒

⇒ v ( 1 - 4 j ) + 4 j v 1 = 0

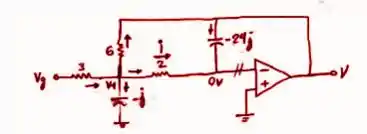
Passo 2

Pessoal lembrando que: Valor eficaz de uma corrente (ou tensão) periódica é sempre uma constante igual à corrente c.c. (ou tensão c.c.) que iria entregar a mesma potência média para um resistor R. Então vamos determinar esse valor :)

V 1 = - j   6 j   1 - 4 j   0   - j   - 6 + 7 j   1 - 9 j   4 j   = 24 + 6 j - 18 - 31 j = 0,7 ∠ 134 , 18 ∘ .

A Corrente máxima: é dada por:

i = v 1 2 = 0,35 ∠ 134 , 18 ∘

i R m s   = 0,35 2 ≈ 0,25 A = 1 4 A

Resposta

1 4 A

Exercícios de Livros Relacionados

Encontre a impedância vista pela fonte ideal de tensão no circuito da Figura P10.53, quando Z o é ajustado para transferência de potência média máxima.
a) Determine a potência média fornecida ao resistor de 8Ω no circuito da Figura P10.37.b) Determine a potência média produzida pela fonte de tensão senoidal ideal.c) Determine Z a b .d) Mostre que a p
Três cargas estão ligadas em paralelo a uma linha de 300 V (ef), como mostra a Figura P10.28. A carga 1 absorve 3 kW com um fp unitário; a carga 2 absorve 5 kVA, com um fp adiantado de 0,8; a carga 3
Uma fábrica absorve 1.600 kW, com um fator de potência atrasado de 0,8. Uma carga adicional de fator de potência variável deve ser instalada na fábrica. A nova carga absorverá 320 kW de potência ativa
Determine a potência média fornecida ao resistor de 5 kV no circuito da Figura P10.61.