Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 24
Calcule o valor eficaz da corrente em regime permanente sobre o resistor de .
Passo 1
E ai gurizada tudo belezinha? Vamos calcular o valor eficaz da corrente em regime permanente sobre o resistor de
Para w=2 temos:
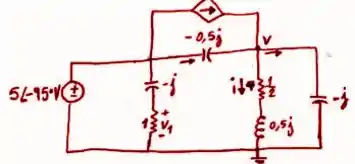
Passo 2
Para circuitos em RPS, sabemos que todas as tensões e correntes do circuito são cossenoidais e de frequência angular igual àquela da excitação. Logo, para determinar essas grandezas elétricas de um circuito em RPS, basta descobrir as amplitudes e fases de cada uma delas. Esse procedimento é facilitado com o uso de fasores.
Resposta
Exercícios de Livros Relacionados
Um grupo de pequenos eletrodomésticos em um sistema de 60 Hz absorve 20 kVA, com um fp atrasado de 0,85, quando funcionam em 125 V (ef). A impedância do alimentador que energiza os eletrodomésticos é
A tensão no início da linha de transmissão da Figura P10.50 é ajustada de modo que o valor eficaz da tensão na carga seja sempre 4.000 V. O capacitor variável é ajustado até que a potência média dissi
As três cargas no Problema 10.28 são alimentadas por uma linha que tem uma impedância em série de 0,02 + j0,05 V, como mostra a Figura P10.29.a) Calcule o valor eficaz da tensão ( V f ) na extremidade
A fonte de tensão senoidal no circuito da Figura P10.60 está operando em uma frequência de 20 krad/s. A reatância capacitiva variável do circuito é ajustada até que a potência média fornecida ao resis
A impedância de carga Z L no circuito da Figura P10.59 é ajustada até que a máxima potência média seja transferida para Z L .a) Especifique o valor de Z L , se N 1 = 3600e s p i r a s e N 2 = 600e s p