Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 64
64. Determine vx e ix no circuito mostrado na Figura 3.107.
Passo 1
Vamos usar a analise de laço, para isso vamos atribuir as correntes de malha:
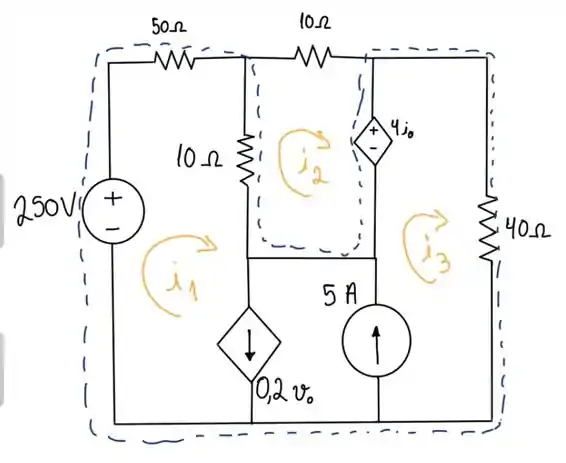
Aquela malhasinha menor que só tem as fontes de correntes não precisamos usar, até porque, se somarmos as duas, podemos pensar naquilo como uma fonte de corrente só. Sempre lembrem que corrente de malha tem sentido horário.
Como temos essas fontes de corrente, no meio dos laços, precisamos definir uma supermalha. A supermalha desse circuito esta circulada de azul, dessa maneira as fontes de corrente não vão estar nela.
Passo 2
Podemos observar que
Começando com o mais simples, vamos usar a LKT para a malha 2:
Substituindo :
Vamos montar a equação interna da supermalha, podemos escrever que:
A imagem nos mostra qual é a tensão , então usando a Lei de Ohm:
Agora, vamos aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) percorrendo a supermalha:
Como
Dividindo por 2:
Passo 3
Agora é só resolver o sistema, podemos usar o MATLAB, uma calculadora, algum outros software, ou até mesmo fazer na mão.
Montando esse sistema com matrizes:
Resolvendo o sistema:
Passo 4
O exercício quer e , calculando:
Já a tensão é igual a: