Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 64
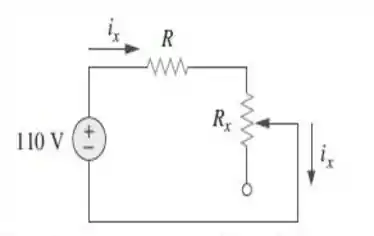
64. O potenciômetro (resistor ajustável) na Figura deve ser projetado para ajustar a corrente de a . Calcule os valores de e para que isso aconteça.
Passo 1
Bom! A primeira coisa que temos que fazer é analisar as condições que esse nosso circuito oferece.
Olha só! A corrente varia de a , sendo o primeiro o valor mínimo e o segundo o valor máximo.
O valor máximo, que é , tá na cara que só vai ocorrer quando
Sendo assim, como a corrente é dada pela divisão da voltagem pela resistência circulante:
Uma vez que sabemos que e , podemos obter o valor de como:
Passo 2
Já quando a resistência está ativa, adquire seu valor mínimo igual a . Desse jeito, como já sabemos o valor de ...
Podemos obter usando o fato de que é dada pela divisão da voltagem pela resistência equivalente, no caso a associação em série entre e :
E voilà! Encontramos nossas respostas!