Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 73

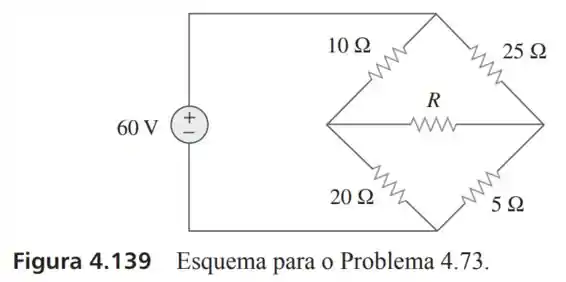
73- Determine a potência máxima que pode ser liberada ao resistor variável R no circuito da Figura 4.139 .

Passo 1

Vamos retirar a resistência R e as fontes independentes para que sejamos capazes de descobrir a resistência de Thévenin do sistema.

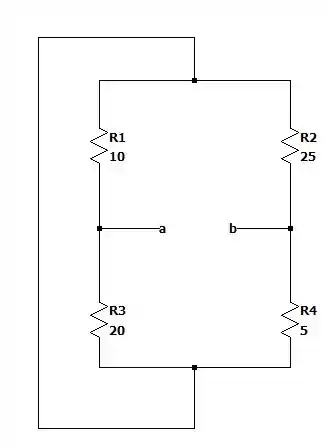
Redesenhando a malha resistiva teremos:

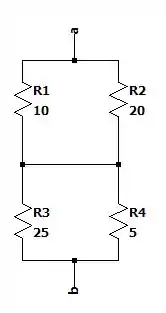
E isso nos dá uma resistência equivalente vale:

R t h = 1 1 10 + 1 20 + 1 1 25 + 1 5 = 1 0.833   Ω

Passo 2

Agora vamos encontrar a tensão de Thévenin e para isso vamos ver o desenho feito.

O valor de i 1 será:

60 = 10 + 20 i 1 → i 1 = 2   A

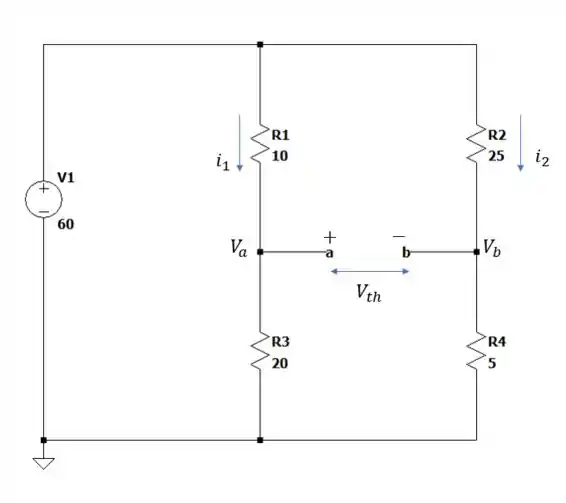
E o de i 2 :

60 = 25 + 5 i 2 → i 2 = 2   A

Dessa forma os valores de V a e V b serão:

60 - V a = 10 i 1 → V a = 60 - 20 = 40   V

60 - V b = 25 i 2 → V b = 60 - 50 = 10   V

Dessa forma o valor da tensão de Thevenin será:

V b a = V t h = V a - V b = 40 - 10 = 30   V

Passo 3

Então a maior potencia será de:

p m a x = V t h 2 4 R t h = 30 2 4 × 10.8333 = 20.77   W

Resposta

p m a x = 20.77   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

64- Obtenha o equivalente de Thévenin visto nos terminais a - b do circuito na Figura 4.130 .
63- Determine o equivalente de Norton para o circuito da Figura 4.129 .
67- O resistor variável R na figura 4.133 é ajustado até absorver a potência máxima do circuito. ( a ) Calcule o valor de R para a potência máxima ( b ) Determine a potência máxima absorvida por R .
66- Determine a potência máxima que pode ser liberada para o resistor R no circuito da Figura 4.132 .
68- Calcule o valor de R que resulta na máxima transferência de potência para o resistor de 10Ω na Figura 4.134 . Determine a potência máxima.