Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 74
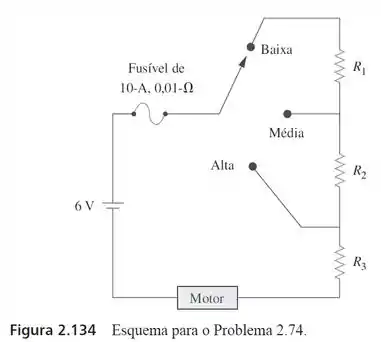
74. O circuito da Figura 2.134 destina-se a controlar a velocidade de um motor de modo que ele absorva correntes de , e , quando a chave se encontrar nas posições alta, média e baixa, respectivamente. O motor pode ser modelado como uma resistência de carga de . Determine as resistências em cascata para queda de tensão , , .
Passo 1
a) Bom! Uma vez que a tensão é dada pelo produto da corrente circulante pela resistência equivalente, usando a seguinte fórmula:
E sabendo que quando a chave está na posição mais baixa, temos que a corrente circulante é de e a resistência equivalente é associação em série entre , , , temos que:
Passo 2
b) Quando a chave está na posição intermediária, temos que a corrente circulante é de e a resistência equivalente é associação em série entre , , e . E como já sabemos o valor de , temos então que:
Passo 3
c) Por último, temos que quando a chave está na posição mais alta, a corrente circulante é de e a resistência equivalente é associação em série entre , , , e . E como já sabemos o valor de e , conseguimos que o nossa resultado vale: