Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 35
35-
Resolva o Problema 4.24 usando o método das correntes de malha.
Passo 1
Então, vamos que vamos bb?!
Pra gente arrasar nessa questão, precisamos analisar o circuito da figura abaixo e usar o método das correntes de malha:
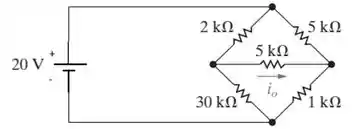
Logo, as equações são:
−20 + 2000(i1 − i2) + 30,000(i1 − i3) = 0
5000i2 + 5000(i2 − i3) + 2000(i2 − i1) = 0
1000i3 + 30,000(i3 − i1) + 5000(i3 − i2) = 0
Passo 2
Passando as equações para a forma padrão, temos:
i1(32000) + i2(−2000) + i3(−30000) = 20
i1(−2000) + i2(12000) + i3(−5000) = 0
i1(−30000) + i2(−5000) + i3(36000) = 0
Resolvendo então:
i1 = 5,5 mA;
i2 = 3 mA;
i3 = 5 mA
Portanto,
io = i3 − i2 = 2 mA.
Resposta
io = 2 mA.
Exercícios de Livros Relacionados
42. Usando a figura 3.88 elabore um problema para ajudar estudantes a entenderem melhor a análise de malhas usando matrizes.
41. Aplique a análise de malhas para determinar i no circuito da Figura 3.87
44. Use a análise de malhas para determinar i 0 no circuito da figura 3.90
43. Use a análise de malhas para determinar v a b e i 0 no circuito da figura 3.89
46. Calcule as correntes de malha i_1 e i_2 na figura 3.92