Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 88
88- Desenvolva as equações de estado para o circuito da Figura .
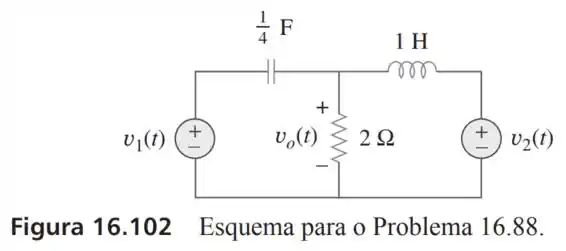
Passo 1
Vamos selecionar como variável de estado a tensão no capacitor e a corrente no indutor da seguinte forma:
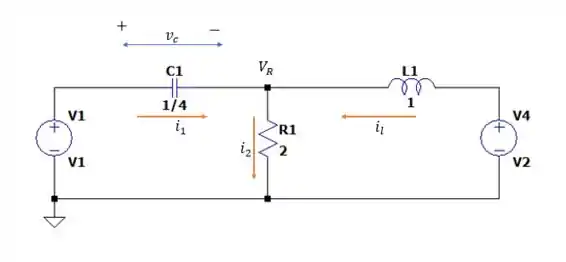
Então a somaória das correntes nos dá:
A tensão no resistor será:
E a corrente será:
Onde:
A corrente no indutor será:
Da equação podemos escrever:
Agora a equação nos deixa com:
Isso nos deixa com a seguinte equação de estado:
Passo 2
Já a equação de saída será:
Ou seja:
Não é muito diferente de dizer que:
Só que chegamos de outro jeito.
Resposta
Exercícios de Livros Relacionados
Se a forma de onda na Figura 7.116a for aplicada ao circuito na Figura 7.116b, determine v ( t ) . Suponha que v ( 0 ) = 0 .
No circuito da Figura 7.117, determine i x para t0 . Seja R 1 = R 2 = 1 k Ω , R 3 = 2 k Ω e C = 0,25m F .
Elabore um problema para ajudar outros estudantes a entenderem melhor as funções de singularidade.
Calcule as integrais a seguir: a∫ 1 t u λ d λ b∫ 0 4 [ r t - 1 ] d t c∫ 1 5 t - 6 2 ⋅ δ t - 2 d t
Expresse os sinais a seguir em termos de funções de singularidade. av t = 0 , t0 - 5 , t0 bi t = 0 , t1 - 10,1t3 10,3t5 0 , t5 cx t = t - 1,1t2 1,2t3 4 - t , 3t4 0 , c a s oc o n t r á r i o á dy t =