Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 50

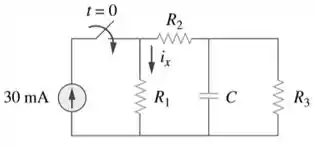
No circuito da Figura 7.117, determine i x para t > 0 . Seja R 1 = R 2 = 1 k Ω , R 3 = 2 k Ω e C = 0,25   m F .

Passo 1

Certo pessoal, sem pânico! É a ultima questão dessa seção então vamo com calma. Primeiro, vamos achar a voltagem do capacitor!

v t = v ∞ + v 0 - v ∞ e - t / τ  

v 0 = 0

Para t > 0 , nós transformamos a fonte de corrente em uma fonte de tensão como mostrado na figura abaixo!

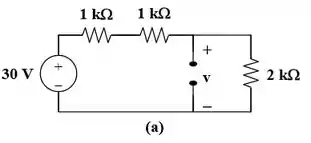
Passo 2

Portanto, vamos calcular os parâmetros de Tau, para jogarmos na formula da tensão!

v ∞ = 2 2 + 1 + 1 30 = 15   V

R t h = 1 + 1 | | 2 = 1 k Ω

τ = R t h C = 10 3 × 1 4 × 10 - 3 = 1 4

Logo

v t = 15 1 - e - 4 t ,   t > 0

Passo 3

Agora obtemos i x de v ( t ) . Considere a figura abaixo.

i x = 30   m A - i T

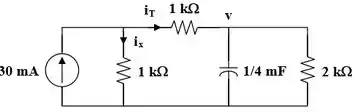
Mas,

i T = v R 3 + C d v d t

i t = 7.5 1 + e - 4 t   m A

Portanto,

i x t = 30 - 7.5 - 7.5 e - 4 t m A

i x t = 7.5 3 - e - 4 t m A ,   t > 0

Resposta

i x t = 7.5 3 - e - 4 t m A ,   t > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se R = 20Ω , L = 0,6H , qual o valor de C que torna o circuito:a) Superamortecidob) Criticamente amortecidoc) Subamortecido
A resposta ao degrau de um circuito R L C é v = 10 + 20 e - 300 t cos ⁡ 400 t - 2 s e n400 t V ,t ≥ 0 Quando o indutor é 50m H . Determine R e C .
A resposta natural de um circuito RLC é descrita pela equação diferencial d 2 v d t ² + 2 d v d t + v = 0 ² Para a qual as condições iniciais são v 0 = 20V e d v 0 d t = 0 . Determine v ( t ) .
Considere o circuito na figura e calcule o valor de R necessário para que a resposta seja criticamente amortecida.
A corrente em um circuito RLC é descrita por d 2 i d t ² + 10 d i d t + 25 i = 0 ² Se i 0 = 2 e d i 0 d t = 0 , determine i ( t ) para t0 .