92. Calcule vs para o transistor na Figura 3.126 dados vo = 4 V,
b = 150 e VBE = 0,7 V.
Passo 1
Podemos definir vários enunciados para a questão, uma deles poderia ser
Considerando o circuito a seguir:
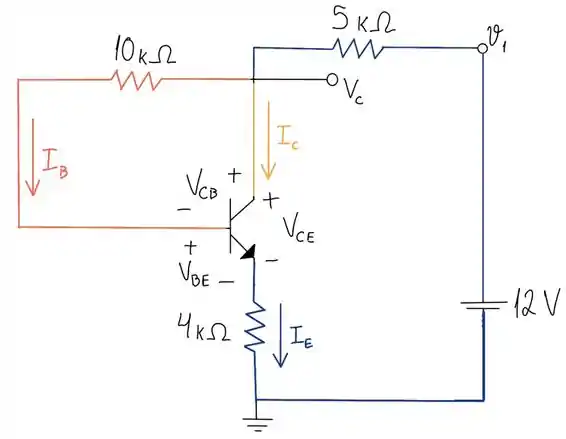
Onde, e . Qual o valor de e de ?
Passo 2
Podemos usar a analise de malhas para resolver. Perceba que:
A parte laranja do circuito é percorrida pela corrente ;
A parte amarela é percorrida pela corrente ;
E a parte azul é percorrida pela corrente
Primeiro vamos aplicar a LKT percorrendo a malha da esquerda, cuidando com a direção das correntes:
Agora vamos aplicar a LKT percorrendo no sentido horário a malha da direita, cuidando da direção das correntes:
Podemos escrever o valor de em função de :
Substituindo:
Nas duas equações temos as tensões que são ingonitas, mas a gente sabe, por se tratar de um transistor, que:
então
Então se somar-mos as duas equações da maneira certa vamos obter uma tensão conhecida.
Vamos isolar a tensão da segunda equação dessa forma:
Agora vamos fazer :
Substituindo os valores conhecidos:
Passo 3
Agora precisamos descobrir a tensão em , para isso vamos calcular a tensão em e descobrir qual é a queda de tensão até chegar em .
Na parte de baixo do circuito foi definido o nó GND, então como temos uma fonte de tensão de , o nó 1 tem a tensão igual a
Depois disso o circuito sofre uma queda de tensão no resistor, então:
Substituindo o valor de :
Conhecemos todas as variáveis da equação: