Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas Abrangentes - Ex. 82
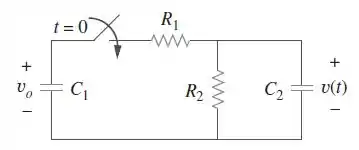
O circuito da Figura é um modelo elétrico das funções corpóreas usadas em faculdades de medicina para estudo de convulsões. Esse modelo tem as seguintes características:
- = Volume de fluido em um medicamento
- = Volume do fluxo sanguíneo em determinada região
- = Resistência oferecida pela entrada do fluxo sanguíneo durante a passagem do medicamento
- = Resistência do mecanismo de excreção, como rins, etc.
- = Concentração inicial da dosagem do medicamento
- = Porcentagem de medicamento presente no fluxo sanguíneo
Determine para , dado que , e .
Passo 1
Pessoal, quando , a função degrau é igual a zero. Assim,
Quando , a chave é fechada e aplicando a lei dos nós no nós entre e :
Multiplicando a equação toda por :
Substituindo os valores,
Passo 2
Quando o circuito atinge o regime permanente, o capacitor atua como um circuito aberto e não há corrente passando por ele. Assim,
Logo,
Substituindo na equação :
Onde é a tensão em regime permanente no capacitor. Como em o degrau unitário é igual a ,
Passo 3
A tensão no capacitor é dada por:
A resistência equivalente do circuito é:
A constante de tempo para o capacitor é dada por:
Substituindo na equação ,
Quando ,
Lá na equação , escrevemos que . Assim,
Substituindo o valor de em ,
Resposta
𝐴 tensão é igual a: