Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 12.Problemas - Ex. 52

Aplique os teoremas do valor inicial e do valor final a cada par de transformadas do Problema 12.42.

Passo 1

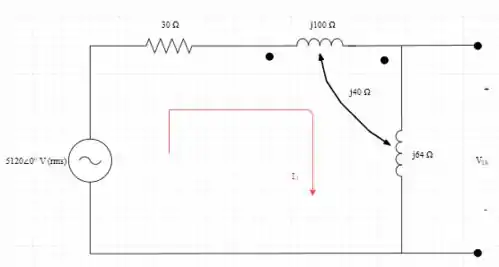
  1. Primeiro desconecte a carga como mostrado na figura

    2. Agora iremos equacionar o circuito

    5120 = 30 I 1 + j 100 I 1 + j 40 I 1 + 64 I 1 + j 40 I 1         1

    Reorganizando

    I 1 = 5120 30 + j 244

    = 2.54   -   j 20.67     A ( r m s

    Agora iremos determinar a tensão de Thevenin através dos terminais

    V T h = j 64 I 1 + j 40 I 1

    = j 140 I 1

    =   j 140 ( 2.54   -   j 20.67

    = 2149.8 + j 264.32 V r m s

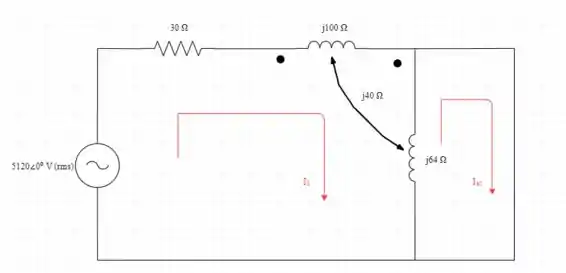
    Conecte os terminais de carga via curto-circuito conforme mostrado na figura

    Agora escreveremos as equações das duas malhas

    5120 = 30 I 1 + j 100 I 1 + j 40 I 1 - I s c + j 64 I 1 - I s c + j 40 I 1       ( 2 )

    0 = j 64 I s c - I 1 - j 40 I 1       ( 3 )

    De (3)

    I 1 = 8 13 I s c       ( 4 )

    Substituindo (4) em (2) para termos a corrente do curto-circuito

    I _ { s c }   =   38.25   -   j 95.63   A ( r m s )

    Agora iremos determinar a impedância de Z T h

    Z T h = V T h V s c

    = 2149.8 + j 264.31 38.25 - j 95.63

    =   5.37   +   j 20.33   Ω

    Passo 2

    A impedância de carga Z 0 t na qual a potência média máxima é transferida para a carga é dada por

    Z 0 = Z T h *

    =   5.37   - j 20.33   Ω

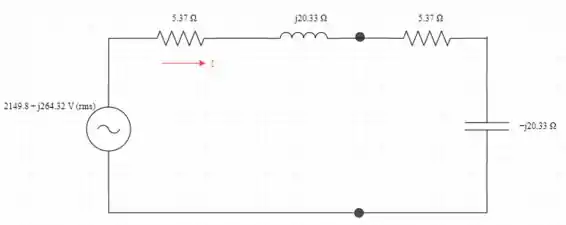
    Conecte o circuito equivalente de Thevenin a Z_{0} conforme mostrado na figura 3

    Agora iremos determinar a corrente que flui através da carga

    I = V T h R T h + R 0

    = 2149.8 + j 264.32 10.74

    = 200.17 + j 24.61 A r m s

    Agora iremos calcular a potência média máxima

    P = I 2 R 0

    = 201.67 2 5.37

    = 218.4   k W

    Passo 3

  2. Aplicando a Lei de Kirchoff no loop 2 da figura

    3. Z 0 I 2 + j 64 I 2 - I 1 - j 40 I 1 = 0

    Então

    I 1 = Z 0 + j 64 j 104 I 2       5

    Onde I 2 é a corrente que flui através da carga dada por

    I 2 = I

    = 200.17 + j 24.61       A r m s

    Substituindo por I 2 em (5) para obtermos I 1

    I 1 = 5.37 - j 20.33 + j 64 j 104 200.17 + j 24.61

    = 85.32 ∠ 0 º       A r m s

    Agora determinando a energia desenvolvida pela fonte de tensão

    S d e v = 5120 ∠ 0 º I 1 *

    = 5120 85.32

    = 436.8   k V A

    Como a parte imaginária da potência complexa é zero, a potência média desenvolvida fornecida pela fonte P d e v é dada por

    P d e v = S d e v

    =   436.8   k W

    Passo 4

  3. A reatância de carga ótima X_{op} é dada por

X o p = - X T h

  =   -   j 20.33   Ω

Então a capacitância de carga ótima Cop é dada por

C o p = 1 w X c

= 1 2 π 60 20.33

= 130.48   μ F

Do apêndice H, o valor de capacitância C 0 mais próximo de C o p é 100   μ F

C o = 100 μ F

Então a indutância de carga X 0 é dada por

X 0 = - 1 2 π 60 100 ∙ 10 - 6

= - 26.5258   Ω

A resistência de carga ótima R o p é dada por

R o p = R T h 2 + X 0 + X T h 2

=   5.37 2 + 20.33 - 26.5258 2

=   8.2   Ω

Do apêndice H, a resistência de carga mais próxima R 0 a R o p é 10   Ω

R 0 = 10   Ω

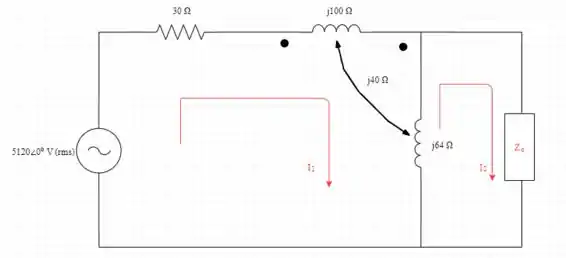
Conecte a impedância de carga Z 0 ao circuito equivalente Thevenin conforme mostrado na figura

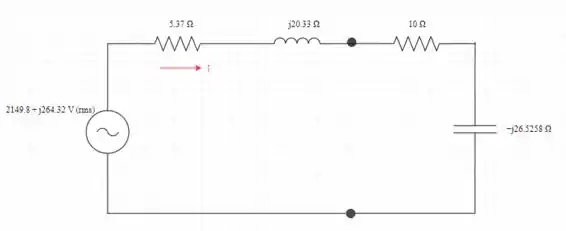
Determine a corrente que flui através da carga I

I = V T h Z T h + Z 0

= 2149.8 + j 264.32 5.37 + j 20.33 + 10 - j 26.5258

= 130.7 ∠ 28.96 º A r m s

Agora iremos determinar a potência média

P = I 2 R 0

= 130.7 2 10

=   170.82   k W

A potência média transferida para a carga é de 170,82 kW em vez de 218,4 kW

C 0 = 100 μ F

R 0 = 10   Ω

Resposta

  1. P   =   218.4   k W
  2. P d e v = 436.8 k W
  3. C 0 = 100 μ F , R 0 = 10   Ω

Exercícios de Livros Relacionados

a) Determine a expressão de V o no domínio da frequência, para o circuito da Figura P13.17. b) Use a expressão no domínio da frequência determinada em (a) para prever os valores inicial e final de v o
A chave no circuito da Figura P13.12 esteve fechada por um longo tempo. Em t = 0, ela é aberta. a) Determine i o, para t $ 0. b) Determine vo, para t $ 0. b) Determine vo, para t $ 0.
Não há nenhuma energia armazenada no circuito da Figura P13.22, em t = 0-. a) Determine Vo. b) Determine vo. c) A solução para vo faz sentido em termos do comportamento conhecido do circuito? Explique
Não há nenhuma energia armazenada no circuito da Figura P13.19, em t = 0 - . a) Use o método das tensões de nó para determinar i 0 . b) Determine a expressão no domínio do tempo para v 0 . c) Suas res
Determine v o no circuito da Figura P13.23, se i g = 20u(t) mA. Não há nenhuma energia armazenada no circuito em t = 0.