Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 53
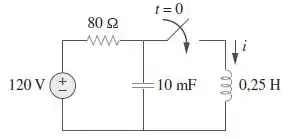
Após estar aberta por um dia, a chave do circuito da Figura é fechada em . Determine a equação diferencial descrevendo , .
Passo 1
Pessoal, vamos lá! O circuito passa um dia inteiro com a chave aberta, com a fonte de tensão alimentando apenas a carga resistiva e a capacitiva. Em regime permanente, o capacitor se comporta como um circuito aberto! Assim, para o instante , temos:
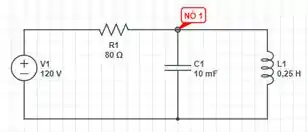
Quando a chave fecha em , temos o seguinte circuito:
Passo 2
Vamos aqui fazer uma análise nodal para a corrente. No nó 1, chega a corrente que se separa em duas: e , certo? Vamos escrever essa equação.
A corrente pode ser escrita como a diferença de tensão entre a fonte e o nó, dividida pela resistência.
A corrente no capacitor pode ser escrita como . Logo,
No entanto, a tensão no nó 1 é igual a tensão em cima do indutor, o que nos leva a escrever . Substituindo essa equação na anterior, temos:
Substituindo os valores de e :
Resposta
A equação é: